背包问题：目标和

#算法/动态规划

目录

• 1. 题目
• 2. 回溯算法思路
  • 2.1. 回溯算法框架
  • 2.2. 选择列表
  • 2.3. 最终代码
• 3. 动态规划思路
  • 3.1. dp 函数定义
  • 3.2. 完整代码
• 4. 转成背包问题
• 5. 总结

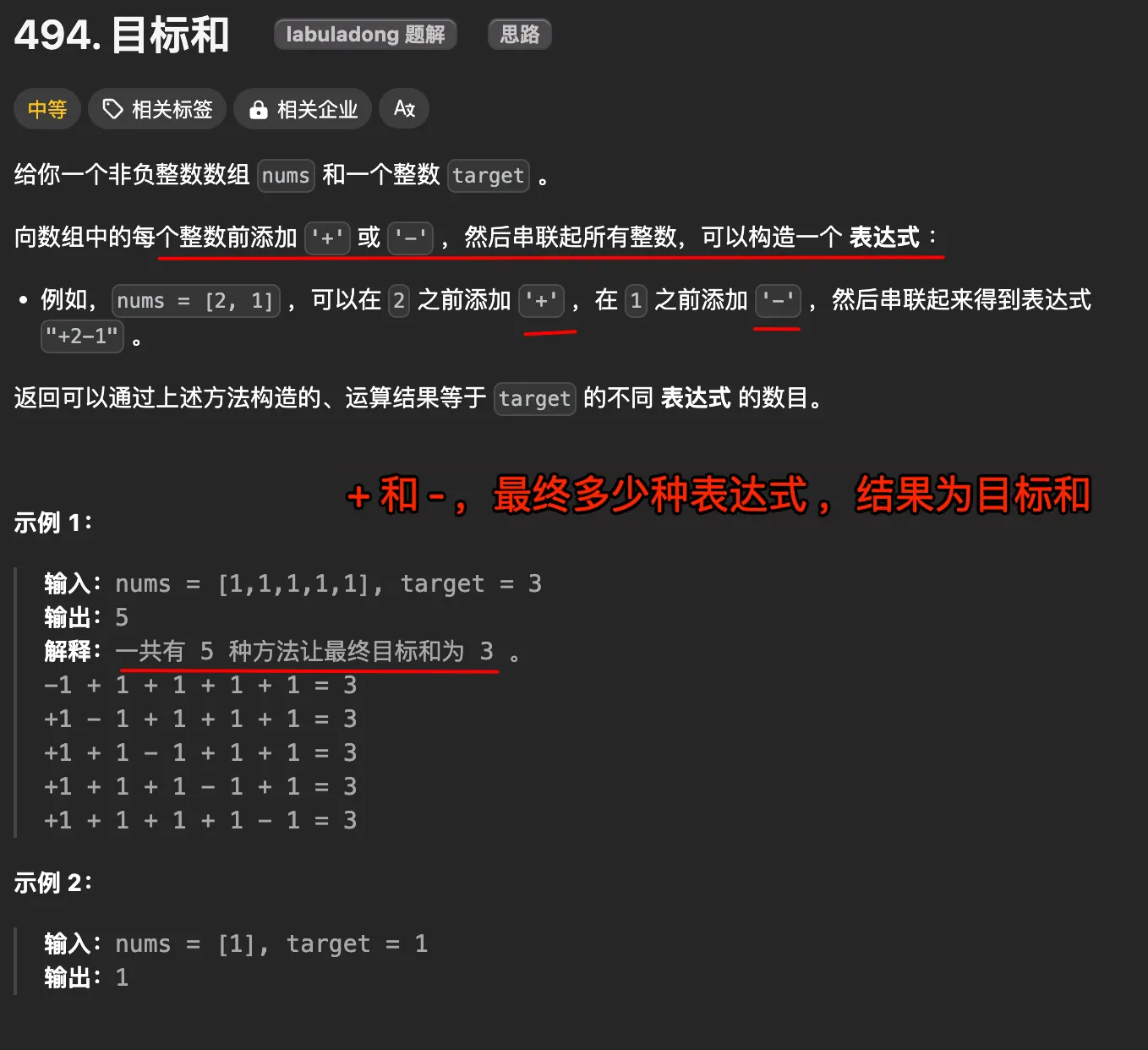
1. 题目

2. 回溯算法思路

2.1. 回溯算法框架

def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

2.2. 选择列表

对于每个数字 nums[i]，我们可以选择

• 给一个正号 + 
• 或者一个负号 -

2.3. 最终代码

var findTargetSumWays = function (nums, target) {
  if (nums.length === 0) return 0;

  var result = 0;
  /**
   * @description 回溯算法模板
   * @param {*} nums 待做选择的数
   * @param {*} i  代表当前做选择的数的下标
   * @param {*} remain  代表剩余的目标值
   * @returns void  无返回值
   */
  function backtrack(nums, i, remain) {
    // base case：如果所有数都计算完了，看看结果是否等于 target
    // 由于 remain 是累加的，所以当 i === nums.length 时，remain === 0 说明恰好凑出 target
    // 更新结果 result
    if (i === nums.length) {
      if (remain === 0) {
        // 说明恰好凑出 target
        result++;
      }
      return;
    }
    /******** 给 nums[i] 选择 - 号 ********/
    // 选择 - , 做加法，
    // 因为目标是凑出 target，所以 remain 需要加上当前的 nums[i]
    remain += nums[i];
    // 穷举 nums[i + 1]
    backtrack(nums, i + 1, remain);
    // 撤销选择
    remain -= nums[i];
    /******** 给 nums[i] 选择 + 号 ********/
    remain -= nums[i];
    // 穷举 nums[i + 1]
    backtrack(nums, i + 1, remain);
    // 撤销选择
    remain += nums[i];
  }
  backtrack(nums, 0, target);
  return result;
};

3. 动态规划思路

3.1. dp 函数定义

// 定义：dp(i, remain) 表示，利用 nums[i..] 这些元素，能够组成和为 remain 的方法数量
dp(nums, i, remain)

3.2. 完整代码

var findTargetSumWays = function (nums, target) {
  if (nums.length === 0) return 0;
  // 备忘录
  const memo = new Map();

  // 定义：利用 nums[i..] 这些元素，能够组成和为 remain 的方法数量
  function dp(nums, i, remain) {
    // base case
    if (i === nums.length) {
      if (remain === 0) return 1;
      return 0;
    }

    // 把它俩转成字符串才能作为哈希表的键
    const key = `${i},${remain}`;

    // 避免重复计算
    if (memo.has(key)) {
      return memo.get(key);
    }

    // 还是穷举
    const result =
      dp(nums, i + 1, remain - nums[i]) + // 选择 - 号
      dp(nums, i + 1, remain + nums[i]); // 选择 + 号

    // 记入备忘录
    memo.set(key, result);
    return result;
  }

  return dp(nums, 0, target);
};

4. 转成背包问题

如果我们把 nums 划分成两个子集 A 和 B，分别代表分配 + 的数和分配 - 的数，那么他们和 target 存在如下关系：

sum(A) - sum(B) = target
sum(A) = target + sum(B)
sum(A) + sum(A) = target + sum(B) + sum(A)
2 * sum(A) = target + sum(nums)

所以问题转成成：nums 中存在几个子集 A，使得 A 中元素的和为 (target + sum(nums)) / 2？

具体省略，更多可参考 https://labuladong.online/algo/dynamic-programming/target-sum/ , 本文只要写出回溯算法即可

5. 总结

• 回溯算法虽好，但是复杂度高，即便消除一些冗余计算，也只是「剪枝」，没有本质的改进。
  • 但有的问题如果实在想不出状态转移方程，尝试用回溯算法暴力解决也是一个聪明的策略，总比写不出来解法强
• 而动态规划就比较玄学了，经过各种改造，从一个加减法问题变成子集问题，又变成背包问题，经过各种套路写出解法，又搞出空间压缩，还得反向遍历。