基本概念：篇二

#算法/图

目录

图相关的名词解释

image.png|536

  • 顶点：

  • 边：

  • 相邻顶点

  • 路径：

  • 度：相邻顶点的个数

    • 入度：顶点的入度是指「指向该顶点的边」的数量；
    • 出度：顶点的出度是指 该顶点指向其他点的边 **的数量。

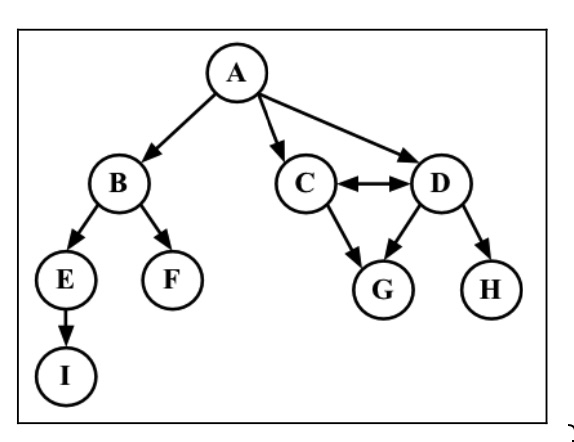
  • 环：

    • 比如ACDA

  • 联通的：

    • 如果图中任何两个顶点都存在路径，那么他是联通的

  • 有向图：如下图

    • image.png|446

  • 强连通：比如上图的 CD，双向都存在路径

  • 无向图：

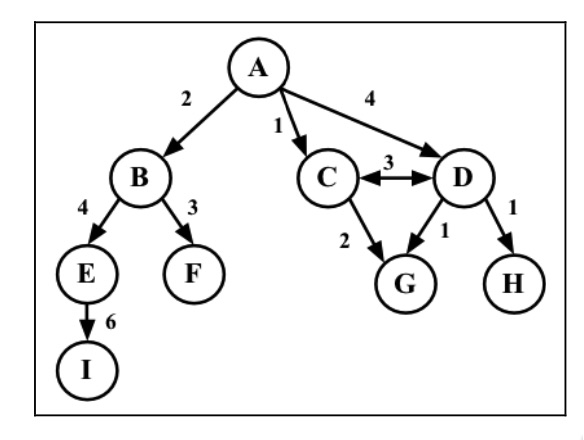
  • 加权图：边赋予权值，如下图

    • image.png|536

图的表示

邻接矩阵

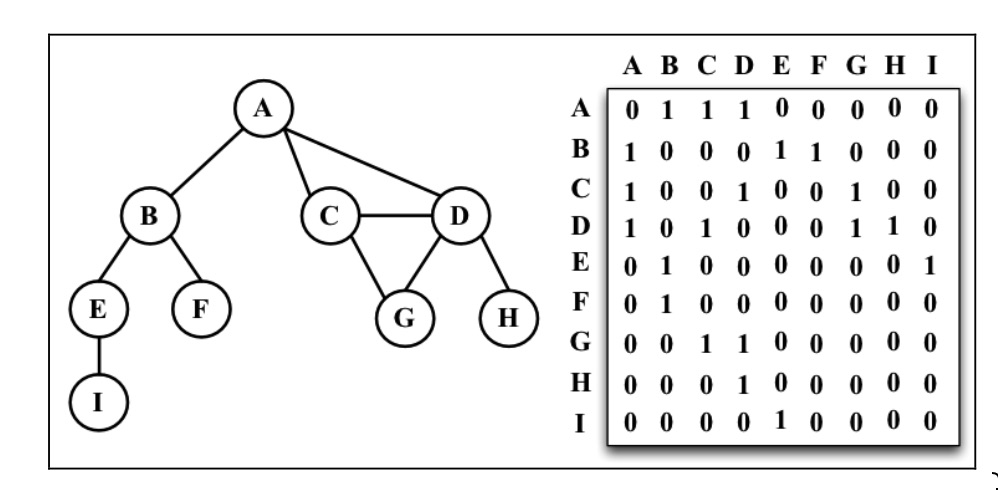
image.png

  • 比较浪费空间
  • 二维数组不够灵活

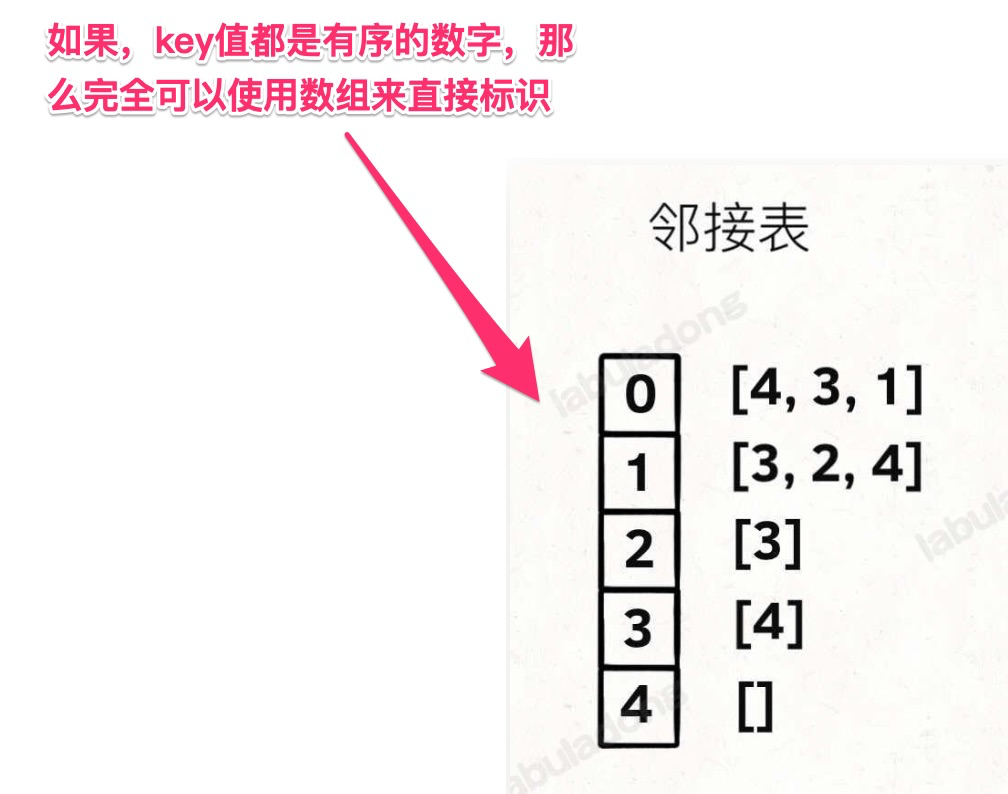
邻接表

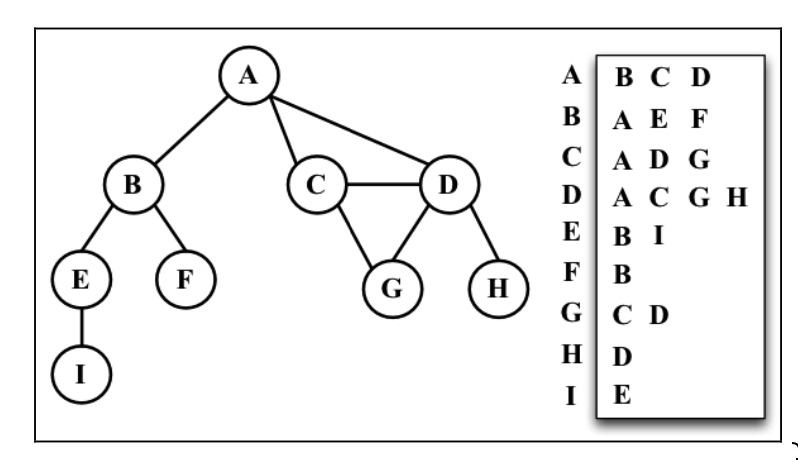
image.png|528

key 为有序的数字

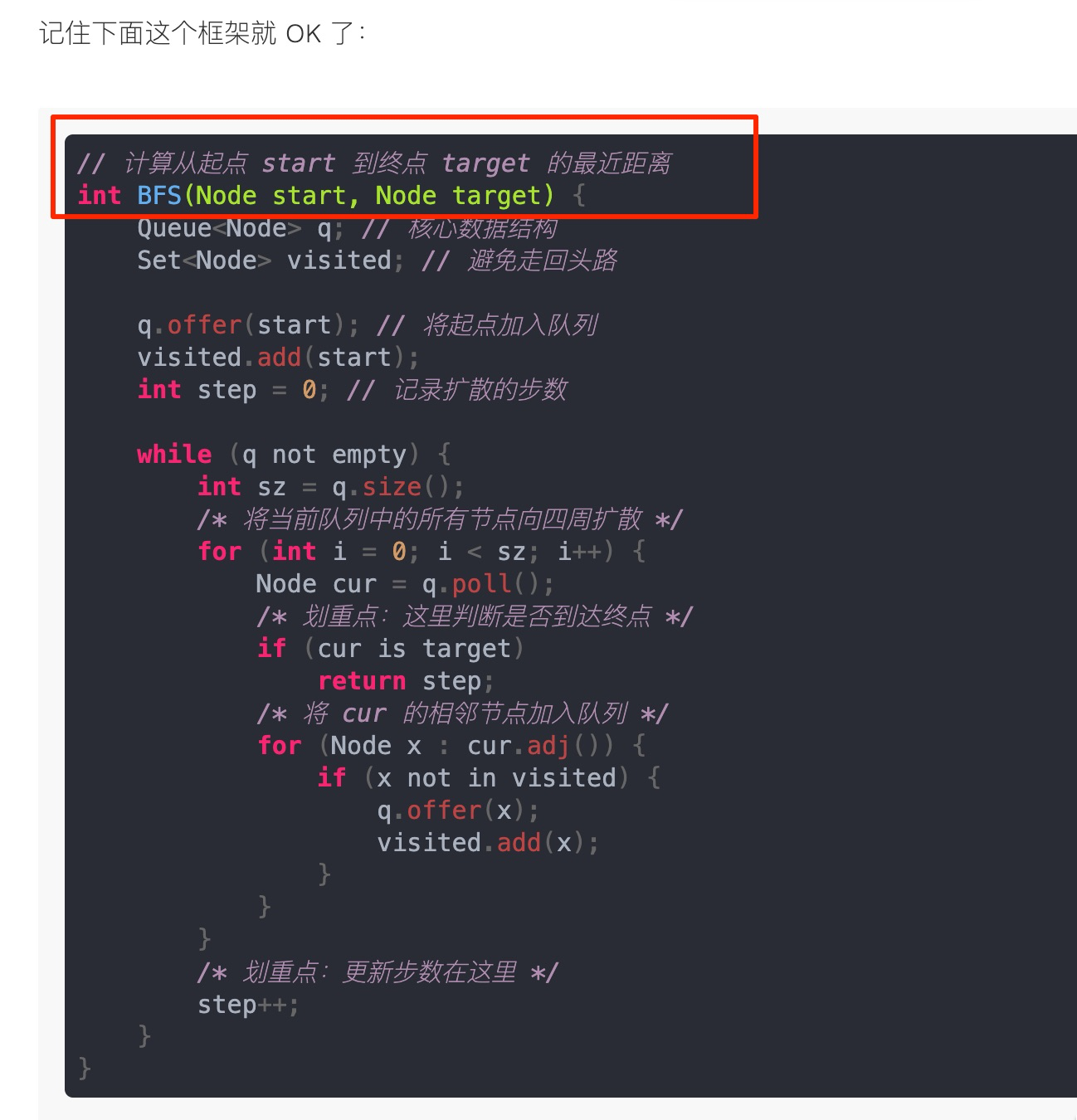
image.png|536

BFS

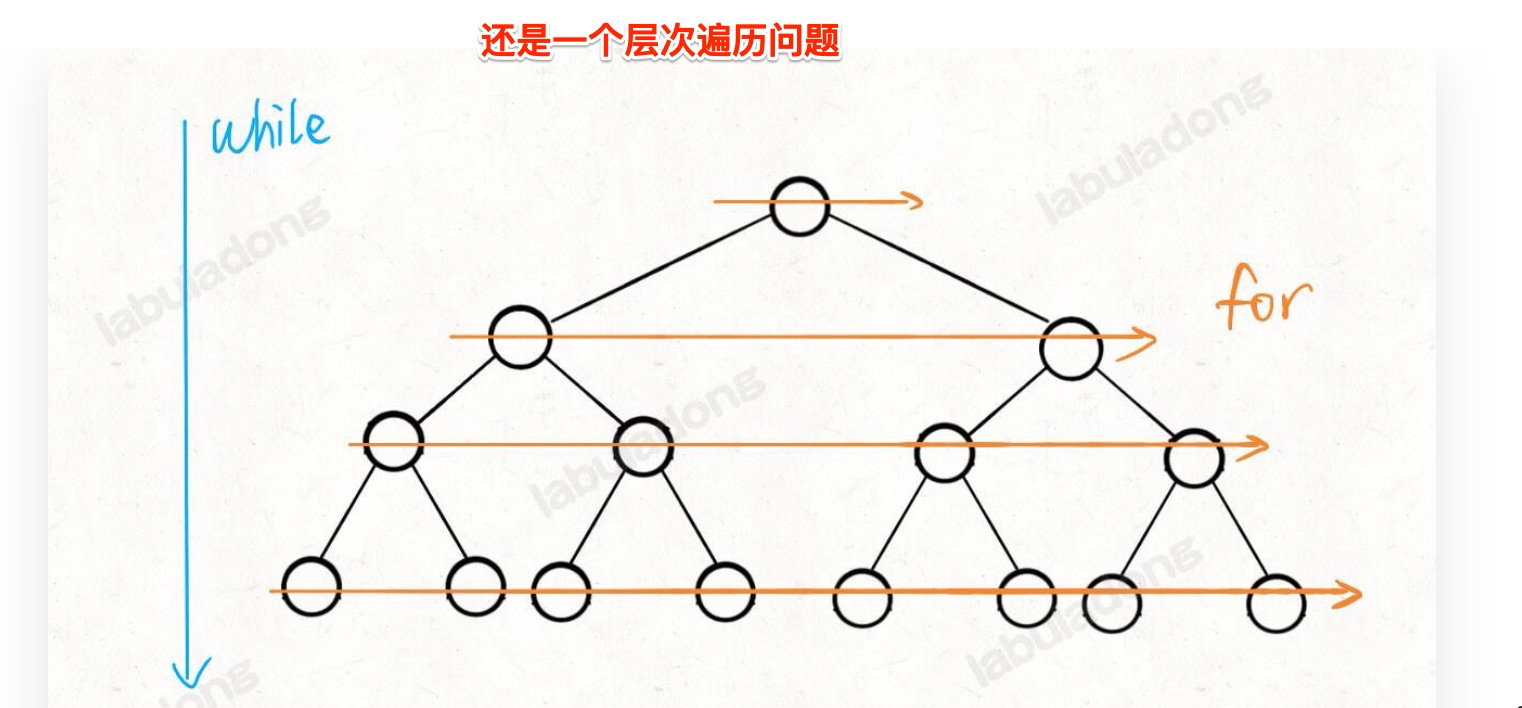
BFS 出现的常见场景好吧，问题的本质就是让你在一幅「图」中找到从起点 **start** 到终点 **target** 的最近距离，这个例子听起来很枯燥，但是 BFS 算法问题其实都是在干这个事儿

框架

image.png

使用JS实现


const BFS = function (start,target) {
    let q = [start]; // 核心数据结构 // 将起点加入队列
    let visited = new Set(); // 避免走回头路
    visited.add(start);
    let step = 0; // 记录扩散的步数
    while (q.length > 0) {
        let sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (let i = 0; i < sz; i++) {
            let cur = q.unshift();
            /* 划重点：这里判断是否到达终点 */
            if (cur === target) return step;
            /* 将 cur 的相邻节点加入队列 */
            for (let x of cur.adj()) {
                if (!visited.has(x)) {
                    q.push(x);
                    visited.add(x);
                }
            }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
};

「 二叉树的最小深度」

image.png

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function (root) {
    if (root == null) {
        return 0;
    }
    let q = [root];
    // root 本身就是一层，depth 初始化为 1
    let depth = 1;
    while (q.length > 0) {
        // 一定要写在这儿！
        const sz = q.length;
        /* 将当前队列中的所有节点向四周扩散 */
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();
            /* 判断是否到达终点 */
            if (cur.left == null && cur.right == null) {
                return depth;
            }

            /* 将 cur 的相邻节点加入队列 */
            if (cur.left != null) {
                q.push(cur.left);
            }
            if (cur.right != null) {
                q.push(cur.right);
            }
        }
        /* 这里增加步数 */
        depth++;
    }
    return depth;
};