图的实现

#算法 #算法/图

目录

• 1. 基本概念
• 2. 图与树的区别
• 3. 图的表示方式：邻接表 + 邻接矩阵
  • 3.1. 节点类型不是 number，而是其他复杂类型怎么办？
  • 3.2. 两种存储方式的区别
    • 3.2.1. 复杂度不同
    • 3.2.2. 邻接矩阵是数学的矩阵
• 4. 有向加权图
• 5. 无向图
• 6. 图 Graph 类定义
  • 6.1. Graph 框架
  • 6.2. 有向加权图（邻接表实现）
  • 6.3. 有向加权图（邻接矩阵实现）
  • 6.4. 无向加权图（邻接表实现）
  • 6.5. 无向加权图（邻接矩阵实现）
• 7. 参考

1. 基本概念

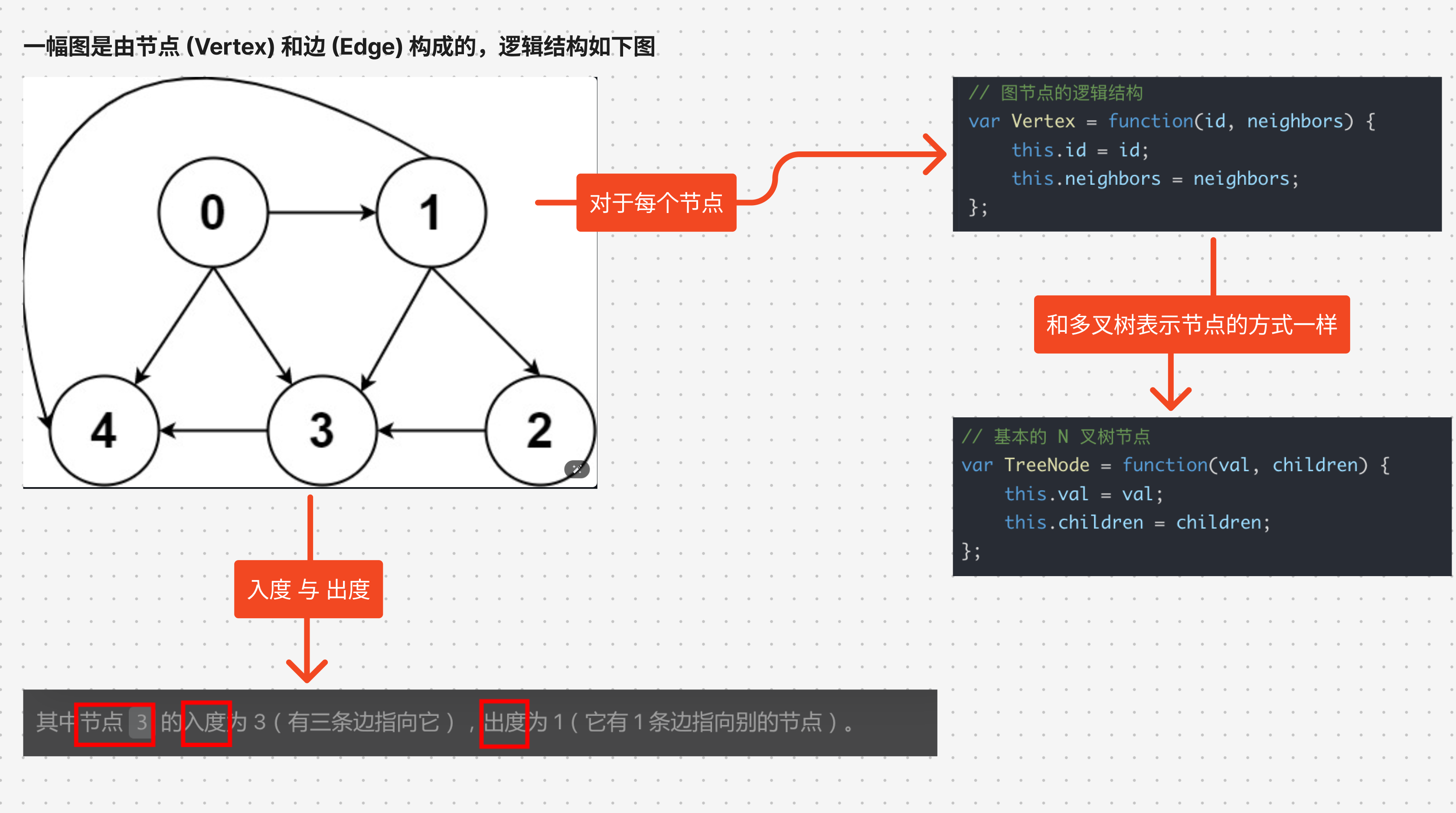
下图中，概括了图最基本的概念，包括

• 节点
• 边
• 出度
• 入度
• 等

2. 图与树的区别

• 在树结构中，只允许父节点指向子节点，不存在子节点指向父节点的情况，子节点之间也不会互相链接
• 而图中没有那么多限制，节点之间可以相互指向，形成复杂的网络结构

3. 图的表示方式：邻接表 + 邻接矩阵

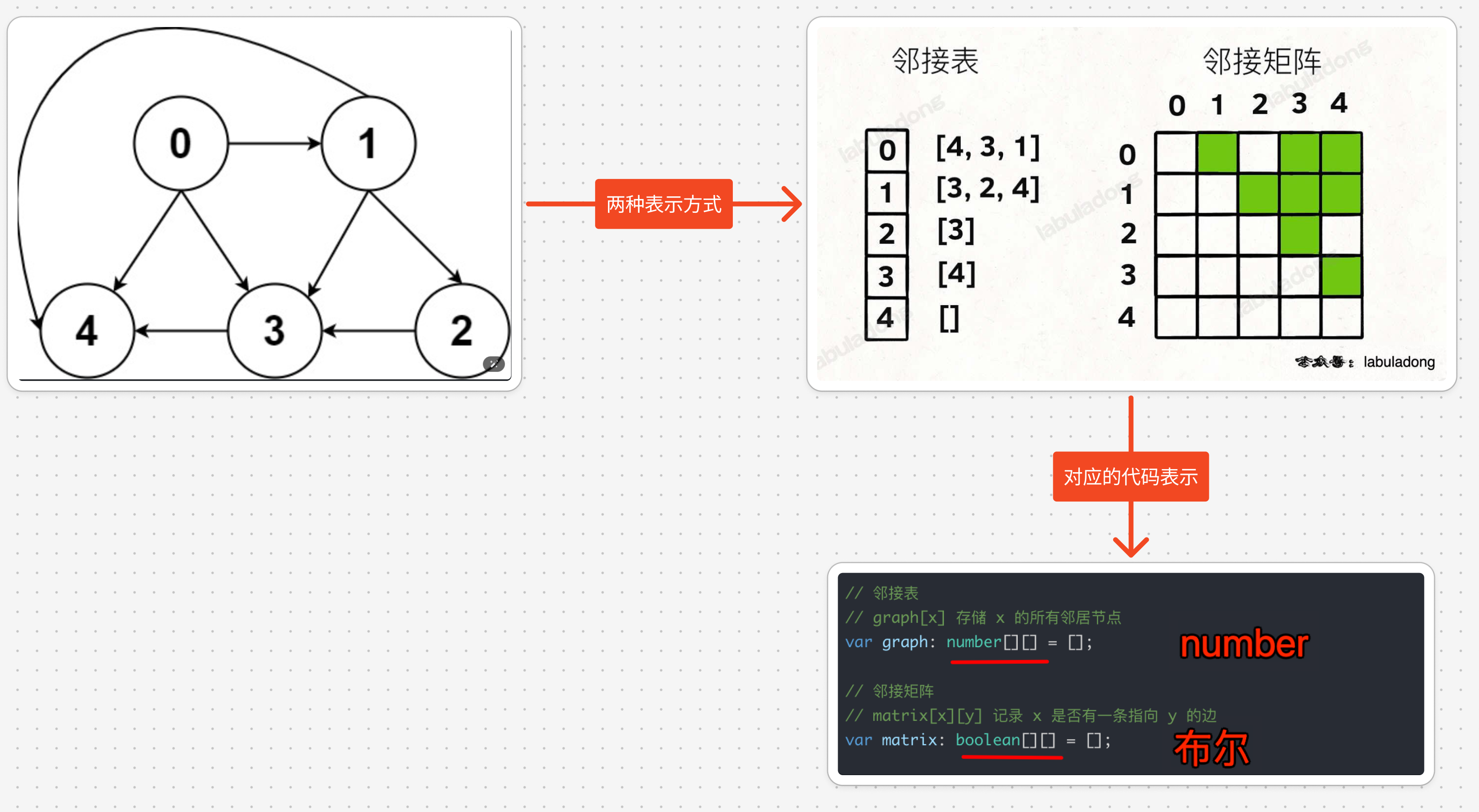
3.1. 节点类型不是 number，而是其他复杂类型怎么办？

很简单，使用哈希

• id 做 key
• value 为其他复杂数据结构

3.2. 两种存储方式的区别

3.2.1. 复杂度不同

对于一幅有 V 个节点，E 条边的图

• 邻接表的空间复杂度是 O(V + E)
• 邻接矩阵的空间复杂度是 O(V^2)。

所以如果一幅图的 E 远小于 V^2（稀疏图），那么邻接表会比邻接矩阵节省空间，反之，如果 E 接近 V^2（稠密图），二者就差不多了。

3.2.2. 邻接矩阵是数学的矩阵

邻接矩阵的最大优势在于，矩阵是一个强有力的数学工具，图的一些隐晦性质可以借助精妙的矩阵运算展现出来。

4. 有向加权图

• 如果是邻接表表示
  • 不仅仅存储某个节点 x 的所有邻居节点
  • 还存储 x 到每个邻居的权重
• 如果是邻接矩阵，matrix[x][y] 不再是布尔值，而是一个 int 值
  • 0 表示没有连接
  • 其他值（非 0）表示权重

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
function Edge(to, weight) {
    this.to = to;
    this.weight = weight;
}
// 注意 Edge
var graph: Edge[][] = [];

// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
var matrix: number[][] = [];

5. 无向图

所谓无向，即双向，如下图：

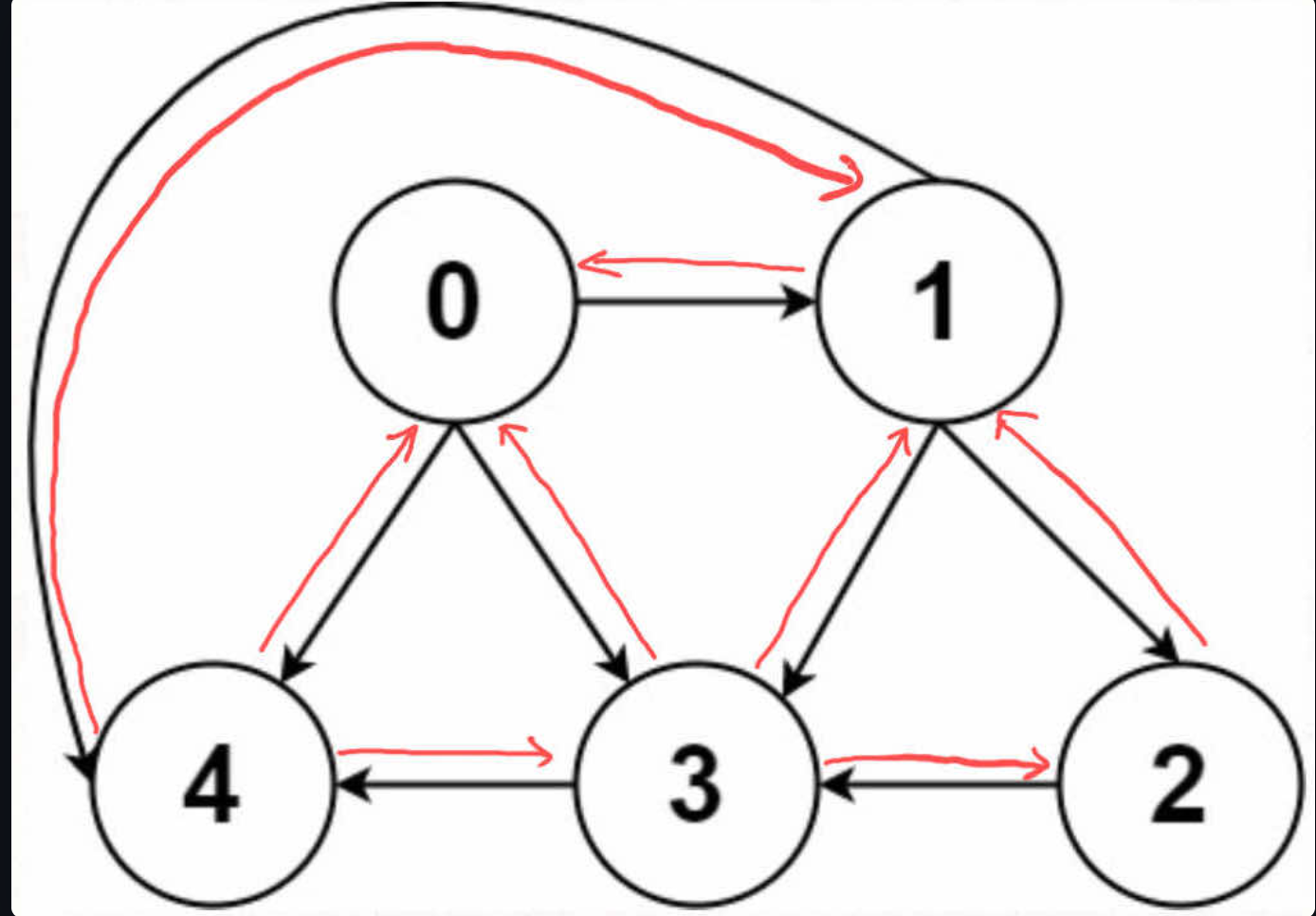
• 邻接矩阵表示无向图：
  • 如果连接无向图中的节点 x 和 y，把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了；
• 邻接表表示无向图：
  • 在 x 的邻居列表里添加 y
  • 同时在 y 的邻居列表里添加 x

6. 图 Graph 类定义

6.1. Graph 框架

class Graph {
  /**
   * @description 添加一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   * @param {number} weight 权重
   */
  addEdge(from, to, weight) {}

  /**
   * @description 移除一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  removeEdge(from, to) {}

  /**
   * @description 判断是否有某条边,即是否有从 from 到 to 的边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  hasEdge(from, to) {}

  /**
   * @description 获取某条边的权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  weight(from, to) {}

  /**
   * @description 获取某个节点的所有邻居节点和对应权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  neighbors(v) {}

  // 返回节点总数
  size() {}
}

neighbors 可以简写为 nb

6.2. 有向加权图（邻接表实现）

// 有向加权图（邻接表实现）
class Graph {
  // 存储相邻节点及边的权重
  // n 为节点数量
  constructor(n) {
    this.graph = Array.from({ length: n }, () => []);
  }

  /**
   * @description 添加一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   * @param {number} weight 权重
   */
  addEdge(from, to, weight) {
    this.graph[from].push({ node: to, weight });
  }

  /**
   * @description 移除一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  removeEdge(from, to) {
    this.graph[from] = this.graph[from].filter((edge) => edge.node !== to);
  }

  /**
   * @description 判断是否有某条边,即是否有从 from 到 to 的边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  hasEdge(from, to) {
    return this.graph[from].some((edge) => edge.node === to);
  }

  /**
   * @description 获取某条边的权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  weight(from, to) {
    return this.graph[from].find((edge) => edge.node === to)?.weight;
  }

  /**
   * @description 获取某个节点的所有邻居节点和对应权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  neighbors(v) {
    return this.graph[v];
  }

  // 返回节点总数
  size() {
    return this.graph.length;
  }
}

6.3. 有向加权图（邻接矩阵实现）

// 有向加权图（邻接矩阵实现）
class Graph {
  // n 为节点数量
  constructor(n) {
    // init matrix
    this.matrix = Array.from({ length: n }, () =>
      Array.from({ length: n }, () => 0),
    );
  }

  /**
   * @description 添加一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   * @param {number} weight 权重
   */
  addEdge(from, to, weight) {
    this.matrix[from][to] = weight;
  }

  /**
   * @description 移除一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  removeEdge(from, to) {
    this.matrix[from][to] = 0;
  }

  /**
   * @description 判断是否有某条边,即是否有从 from 到 to 的边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  hasEdge(from, to) {
    return this.matrix[from][to] > 0;
  }

  /**
   * @description 获取某条边的权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  weight(from, to) {
    return this.matrix[from][to];
  }

  /**
   * @description 获取某个节点的所有邻居节点和对应权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  neighbors(v) {
    const res = [];
    for (let i = 0; i < this.matrix[v].length; i++) {
      if (this.matrix[v][i] > 0) {
        res.push({ node: i, weight: this.matrix[v][i] });
      }
    }
    return res;
  }

  // 返回节点总数
  size() {
    return this.matrix.length;
  }
}

6.4. 无向加权图（邻接表实现）

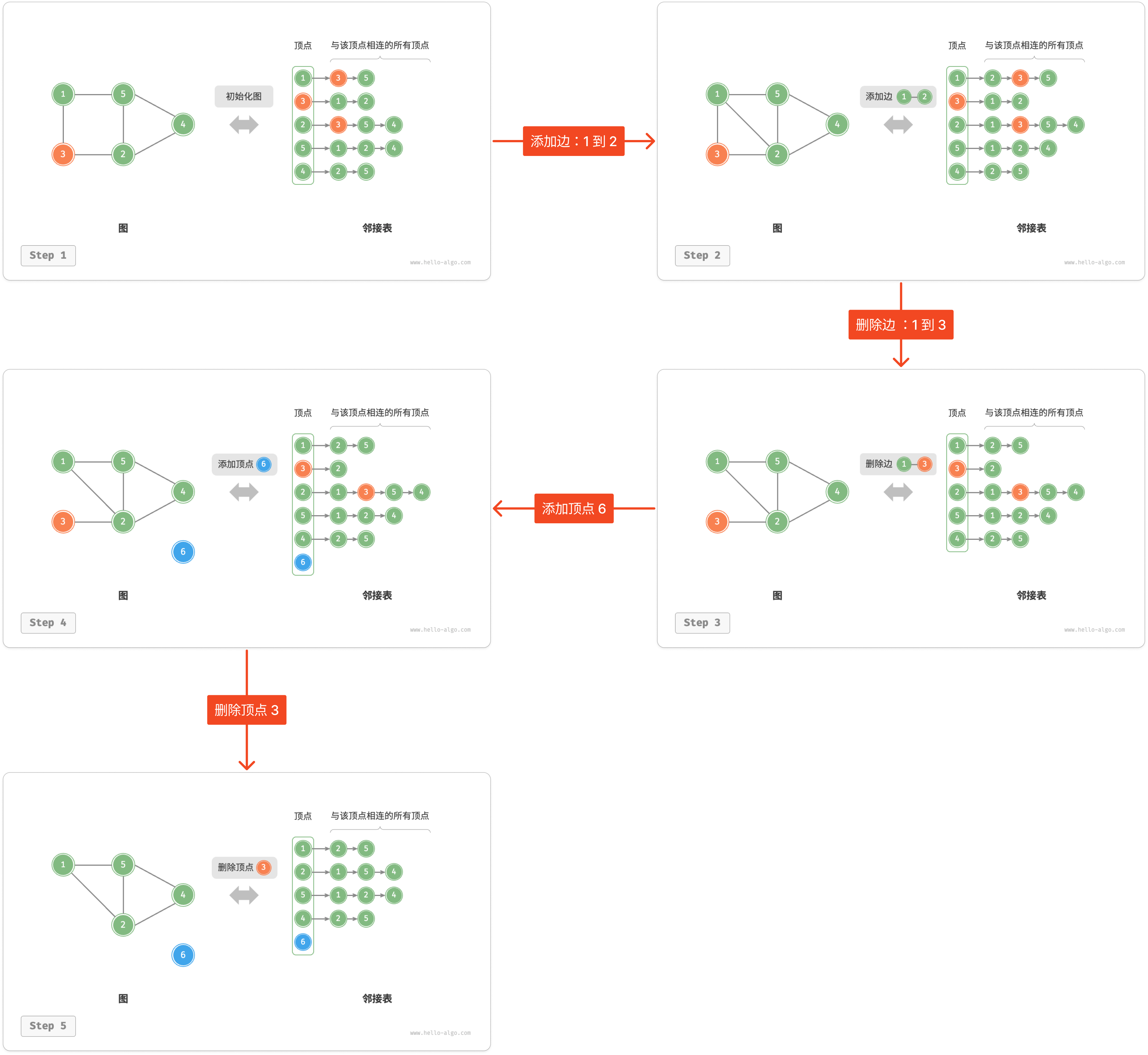
基于 #有向加权图（邻接表实现） 只需要添加以下两行代码即可

// 无向加权图（邻接表实现）
class Graph {
  // 存储相邻节点及边的权重
  // n 为节点数量
  constructor(n) {
    this.graph = Array.from({ length: n }, () => []);
  }

  /**
   * @description 添加一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   * @param {number} weight 权重
   */
  addEdge(from, to, weight) {
    this.graph[from].push({ node: to, weight });
    this.graph[to].push({ node: from, weight });
  }

  /**
   * @description 移除一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  removeEdge(from, to) {
    this.graph[from] = this.graph[from].filter((edge) => edge.node !== to);
    this.graph[to] = this.graph[to].filter((edge) => edge.node !== from);
  }

  /**
   * @description 判断是否有某条边,即是否有从 from 到 to 的边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  hasEdge(from, to) {
    return this.graph[from].some((edge) => edge.node === to);
  }

  /**
   * @description 获取某条边的权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  weight(from, to) {
    return this.graph[from].find((edge) => edge.node === to)?.weight;
  }

  /**
   * @description 获取某个节点的所有邻居节点和对应权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  neighbors(v) {
    return this.graph[v];
  }

  // 返回节点总数
  size() {
    return this.graph.length;
  }
}

6.5. 无向加权图（邻接矩阵实现）

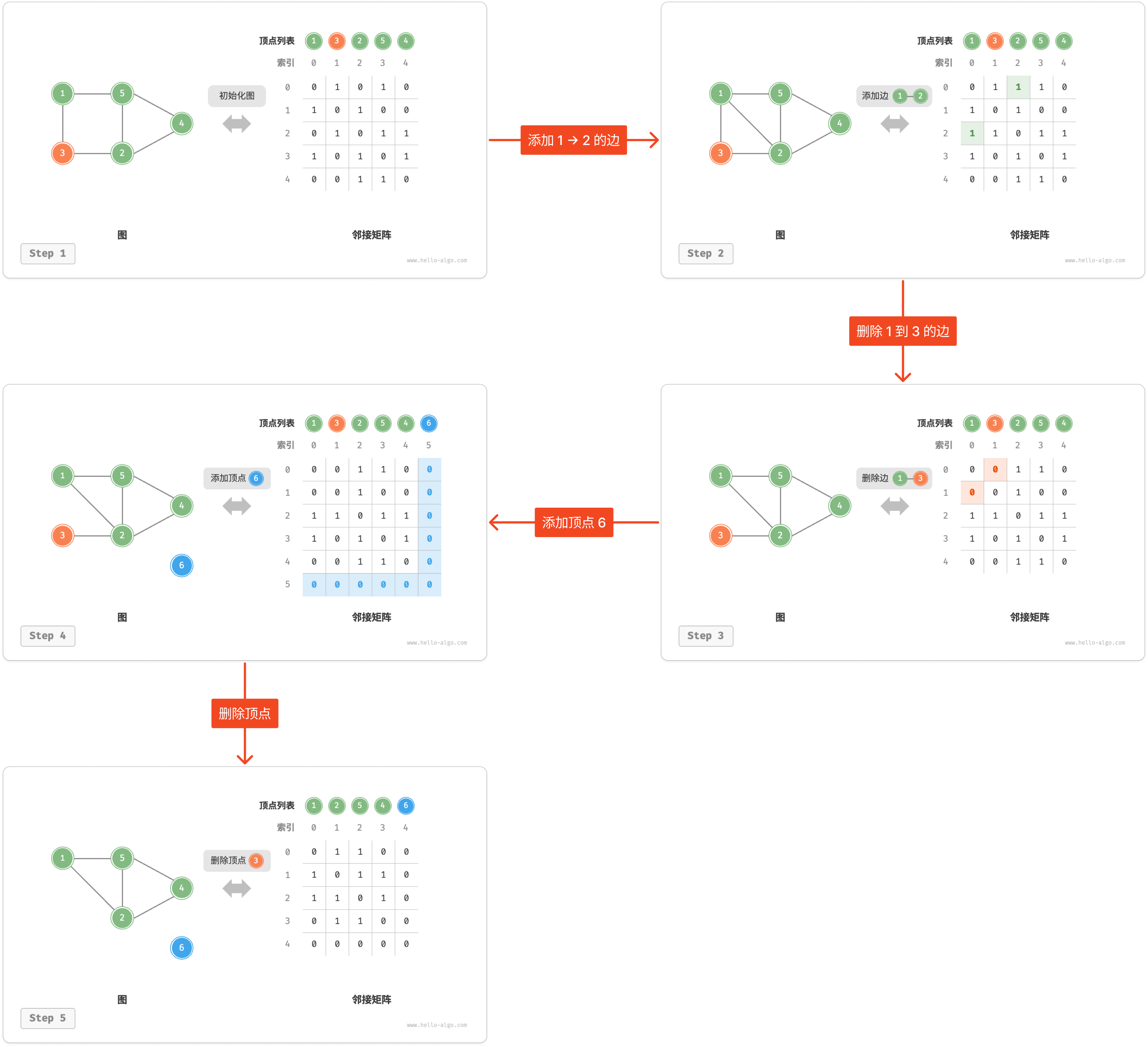
在 #6.3. 有向加权图（邻接矩阵实现）中添加两行代码即可，如下：

// 无向加权图（邻接矩阵实现）
class Graph {
  // n 为节点数量
  constructor(n) {
    // init matrix
    this.matrix = Array.from({ length: n }, () =>
      Array.from({ length: n }, () => 0),
    );
  }

  /**
   * @description 添加一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   * @param {number} weight 权重
   */
  addEdge(from, to, weight) {
    this.matrix[from][to] = weight;
    this.matrix[to][from] = weight;
  }

  /**
   * @description 移除一条边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  removeEdge(from, to) {
    this.matrix[from][to] = 0;
    this.matrix[to][from] = 0;
  }

  /**
   * @description 判断是否有某条边,即是否有从 from 到 to 的边
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  hasEdge(from, to) {
    return this.matrix[from][to] > 0;
  }

  /**
   * @description 获取某条边的权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  weight(from, to) {
    return this.matrix[from][to];
  }

  /**
   * @description 获取某个节点的所有邻居节点和对应权重
   * @param {string} from 起始节点
   * @param {string} to 目标节点
   */
  neighbors(v) {
    const res = [];
    for (let i = 0; i < this.matrix[v].length; i++) {
      if (this.matrix[v][i] > 0) {
        res.push({ node: i, weight: this.matrix[v][i] });
      }
    }
    return res;
  }

  // 返回节点总数
  size() {
    return this.matrix.length;
  }
}

7. 参考

• https://labuladong.online/algo/data-structure-basic/graph-basic/
• https://labuladong.online/algo/data-structure-basic/graph-traverse-basic/