子序列：最大子数组

#算法/动态规划

目录

• 1. 题目
• 2. 解法一：滑动窗口解法
• 3. 解法二：动态规划解法
• 4. 解法三：前缀和思路

1. 题目

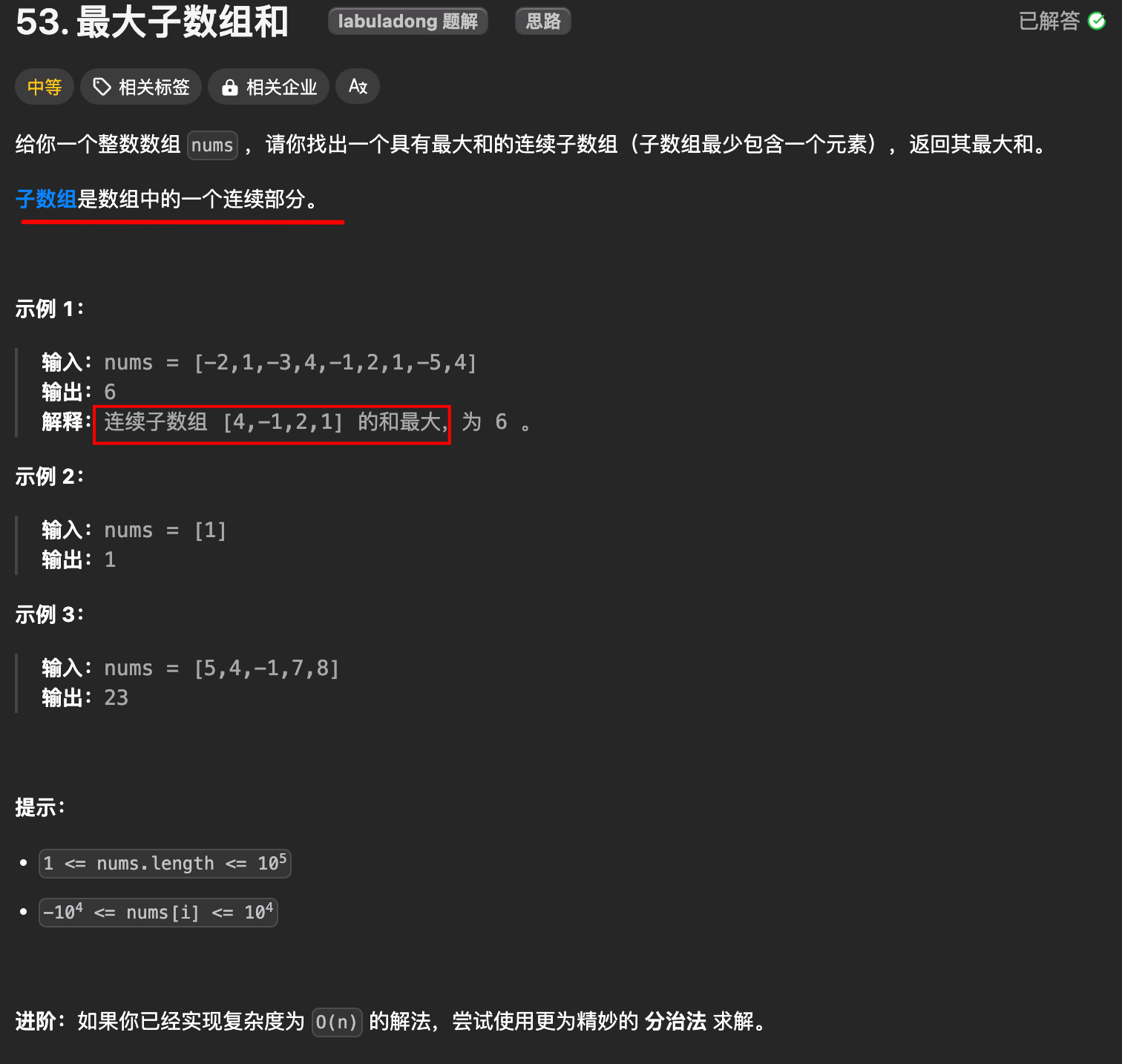
2. 解法一：滑动窗口解法

• 在窗口内元素之和大于等于 0 时扩大窗口
• 在窗口内元素之和小于 0 时缩小窗口
• 在每次移动窗口时更新答案

请问：有正数有负数为什么也能得到正确答案？

/**
 * @description 最大子数组和，滑动窗口思路
 * @param {number[]} nums
 * @return {number} 返回最大子数组和
 */
var maxSubArray = function (nums) {
  // 题设中的最小值
  let res = -10000 * 100000;
  // ①  初始化左指针，右指针，窗口内元素的和
  let left = 0; // 左指针
  let right = 0; // 右指针
  let windowSum = 0; // 窗口内元素的和

  // ②  遍历，使用滑动窗口思路
  while (right < nums.length) {
    // ③  更新 windowSum
    windowSum += nums[right];
    // ④  更新右指针
    right++;
    // ⑤  更新结果
    res = Math.max(res, windowSum);
    // ⑥  判断是否需要收缩左指针
    // 如果 windowSum 小于 0，说明 windowSum 对结果是减少的，需要收缩左指针
    while (windowSum < 0) {
      // ⑦  更新 windowSum
      windowSum -= nums[left];
      left++;
    }
  }

  return res;
};

3. 解法二：动态规划解法

以 nums[i] 为结尾的「最大子数组和」为 dp[i]

dp[i] 有两种「选择」

• 要么与前面的相邻子数组连接，形成一个和更大的子数组；
• 要么不与前面的子数组连接，自成一派，自己作为一个子数组

var maxSubArray = function (nums) {
  var n = nums.length;
  if (n === 0) return 0;
  // 定义：dp[i] 记录以 nums[i] 为结尾的「最大子数组和」
  var dp = new Array(n);
  // base case
  // 第一个元素前面没有子数组
  dp[0] = nums[0];
  // 状态转移方程
  for (var i = 1; i < n; i++) {
    dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
  }
  // 得到 nums 的最大子数组
  var res = -Infinity;
  for (var i = 0; i < n; i++) {
    res = Math.max(res, dp[i]);
  }
  return res;
};

还可以进一步压缩空间，略！

4. 解法三：前缀和思路

// 前缀和技巧解题
var maxSubArray = function (nums) {
  var n = nums.length;
  var preSum = new Array(n + 1).fill(0);
  preSum[0] = 0;
  // 构造 nums 的前缀和数组
  for (var i = 1; i <= n; i++) {
    preSum[i] = preSum[i - 1] + nums[i - 1];
  }

  var res = Number.NEGATIVE_INFINITY;
  var minVal = Number.POSITIVE_INFINITY;
  for (var i = 0; i < n; i++) {
    // 维护 minVal 是 preSum[0..i] 的最小值
    minVal = Math.min(minVal, preSum[i]);
    // 以 nums[i] 结尾的最大子数组和就是 preSum[i+1] - min(preSum[0..i])
    res = Math.max(res, preSum[i + 1] - minVal);
  }
  return res;
};