子序列:最小编辑距离
#算法/动态规划
目录
题目

分析
解决两个字符串的动态规划问题,一般都是用两个指针 i, j 分别指向两个字符串的最后,然后一步步往前移动,缩小问题的规模,如下面动动图:
s1 = "rad"s2 = "apple"
把 s1 变成 s2

其实一共 4 种操作:
- 啥都别做(
skip),直接移动i和j即可。 - 插入(
insert) - 删除(
delete) - 替换(
replace)
定义 dp 函数:dp(s1, i, s2, j) ,代表 s1[0..i] 和 s2[0..j] 的最小编辑距离,即 s1 变成 s2 的 最短编辑距离。
注意:这里是倒着递归
自顶向下的递归解法 - 暴力
var minDistance = function (s1, s2) {
var m = s1.length, n = s2.length;
// i,j 初始化指向最后一个索引
return dp(s1, m - 1, s2, n - 1);
};
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
var dp = function (s1, i, s2, j) {
// base case
// :::: 即 s1 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s2 的长度,
// 即一直插入
if (i === -1) return j + 1;
// :::: 即 s2 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s1 的长度,
// 即一直删除
if (j === -1) return i + 1;
// skip, 所以 i-1, j-1
if (s1[i] === s2[j]) {
return dp(s1, i - 1, s2, j - 1);
}
return Math.min(
// 插入, s1[i] 插入到 s2[j] 前面, 所以 j-1
dp(s1, i, s2, j - 1) + 1,
// 删除,s1[i] 删除,所以 i-1
dp(s1, i - 1, s2, j) + 1,
// 替换, s2[j] 替换为 s1[i], 所以 i-1, j-1
dp(s1, i - 1, s2, j - 1) + 1
);
};
console.log(minDistance('horse', 'ros')); // 3
console.log(minDistance('intention', 'execution')); // 5
[!tip] 注意看注释,另外这里的
状态与选择分别是什么?
[!tip] LeetCode 执行超时!
自顶向下的递归解法 - 备忘录优化
var minDistance = function (s1, s2) {
var m = s1.length, n = s2.length;
const memo = [];
for (let i = 0; i < m; i++) {
memo[i] = new Array(n).fill(-1);
}
// i,j 初始化指向最后一个索引
return dp(s1, m - 1, s2, n - 1, memo);
};
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
var dp = function (s1, i, s2, j, memo) {
// base case
// :::: 即 s1 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s2 的长度,
// 即一直插入
if (i === -1) return j + 1;
// :::: 即 s2 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s1 的长度,
// 即一直删除
if (j === -1) return i + 1;
// memo[i][j] 已经计算过
if (memo[i][j] !== -1) return memo[i][j];
// skip, 所以 i-1, j-1
if (s1[i] === s2[j]) {
return memo[i][j] = dp(s1, i - 1, s2, j - 1, memo);
}
return memo[i][j] = Math.min(
// 插入, s1[i] 插入到 s2[j] 前面, 所以 j-1
dp(s1, i, s2, j - 1, memo) + 1,
// 删除,s1[i] 删除,所以 i-1
dp(s1, i - 1, s2, j, memo) + 1,
// 替换, s2[j] 替换为 s1[i], 所以 i-1, j-1
dp(s1, i - 1, s2, j - 1, memo) + 1
);
};
console.log(minDistance('horse', 'ros'));
console.log(minDistance('intention', 'execution'));
也直接使用memo={} 或者 memo=new Map() 来优化,避免初始化二维数组,如下代码:
var minDistance = function (s1, s2) {
var m = s1.length, n = s2.length;
// 直接使用对象,而不是二维数组
const memo = {};
// i,j 初始化指向最后一个索引
return dp(s1, m - 1, s2, n - 1, memo);
};
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
var dp = function (s1, i, s2, j, memo) {
// base case
// :::: 即 s1 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s2 的长度,
// 即一直插入
if (i === -1) return j + 1;
// :::: 即 s2 = '' ,所以 s1 变成 s2 的最小编辑距离就是 s1 的长度,
// 即一直删除
if (j === -1) return i + 1;
// memo[i][j] 已经计算过
if (memo[`${i}-${j}`] !== undefined) return memo[`${i}-${j}`];
// skip, 所以 i-1, j-1
if (s1[i] === s2[j]) {
return memo[`${i}-${j}`] = dp(s1, i - 1, s2, j - 1, memo);
}
return memo[`${i}-${j}`] = Math.min(
// 插入, s1[i] 插入到 s2[j] 前面, 所以 j-1
dp(s1, i, s2, j - 1, memo) + 1,
// 删除,s1[i] 删除,所以 i-1
dp(s1, i - 1, s2, j, memo) + 1,
// 替换, s2[j] 替换为 s1[i], 所以 i-1, j-1
dp(s1, i - 1, s2, j - 1, memo) + 1
);
};
console.log(minDistance('horse', 'ros'));
console.log(minDistance('intention', 'execution'));
[!danger] 注意:一点要在所有需要赋值给
memo的地方赋值,搞了半天,发现少了赋值了
[!info] 如果说
memo为对象时,可以少了初始化工作,如果是数组时,初始化数组时,其实保证二维数组长度和宽度大一点也没关系。
至底向上的 dp table 解法

[!warning]
dp 函数的 base case 是 i, j 等于-1,而 dp数组索引至少是 0,所以 dp 数组会偏移一位。
代码如下:
let minDistance = function (s1, s2) {
let m = s1.length, n = s2.length;
// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]
let dp = [];
for (let i = 0; i <= m; i++) {
dp[i] = new Array(n + 1).fill(0);
}
// base case
// ::::即 s2 = ''
for (let i = 1; i <= m; i++) {
dp[i][0] = i;
}
// ::::即 s1 = ''
for (let j = 1; j <= n; j++) {
dp[0][j] = j;
}
// 自底向上求解
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (s1[i - 1] === s2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
);
}
}
}
// 储存着整个 s1 和 s2 的最小编辑距离
return dp[m][n];
};
[!failure] 其实,dp数组,保证开始索引
大于 0,最大等于 length + 1即能保证范围正常,虽然大一点也行
空间复杂度压缩成 O(min(M, N))
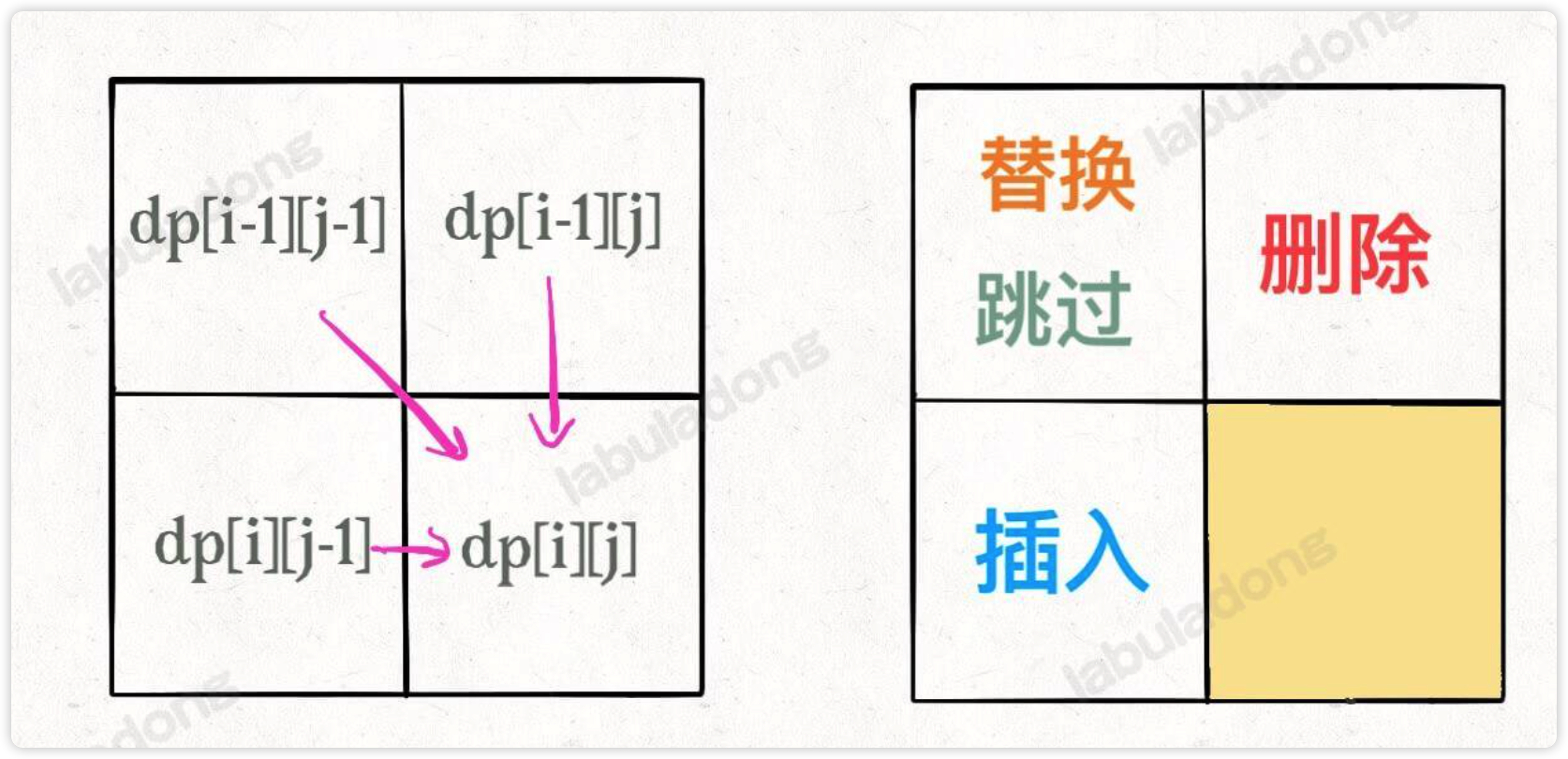
如上图,既然每个 dp[i][j] 只和它附近的三个状态有关,空间复杂度是可以压缩成 O(min(M, N)) 的(M,N 是两个字符串的长度)
数据结构构造如下:
function Node() {
this.val = 0;
this.choice = 0; // 0 代表啥都不做
// 1 代表插入
// 2 代表删除
// 3 代表替换
}
val 属性就是之前的 dp 数组的数值,choice 属性代表操作。在做最优选择时,顺便把操作记录下来,然后就从结果反推具体操作。
我们的最终结果不是 dp[m][n] 吗,这里的 val 存着最小编辑距离,choice 存着最后一个操作,比如说是插入操作,那么就可以左移一格
最终,到 dp[0][0],如下图这样:

具体实现不展开,点到为止!
最后
- 这个题主要是
倒着遍历 - 还是
递归备忘录,不容易写出问题,dp 数组细节比较多 - 最后,还有个思路是如何
压缩空间复杂度,取决于状态如何转移? 很多动态规划的问题都可以压缩空间复杂度