最小生成树： Kruskal 算法

目录

• 最小生成图定义
• 图生成树的合法性
• Kruskal 算法（克鲁斯卡尔算法）
• 例题一：最低成本连通所有城市
• 例题二：

最小生成图定义

• 树和图的根本区别：
  • 树不会包含环
  • 图可以包含环
• 无环连通图
  • 树一种特殊的图
• 生成树
  • ① 在图中找一棵==包含图中的所有节点==的树。
  • ② 含有图中==所有顶点==的==无环连通子图==

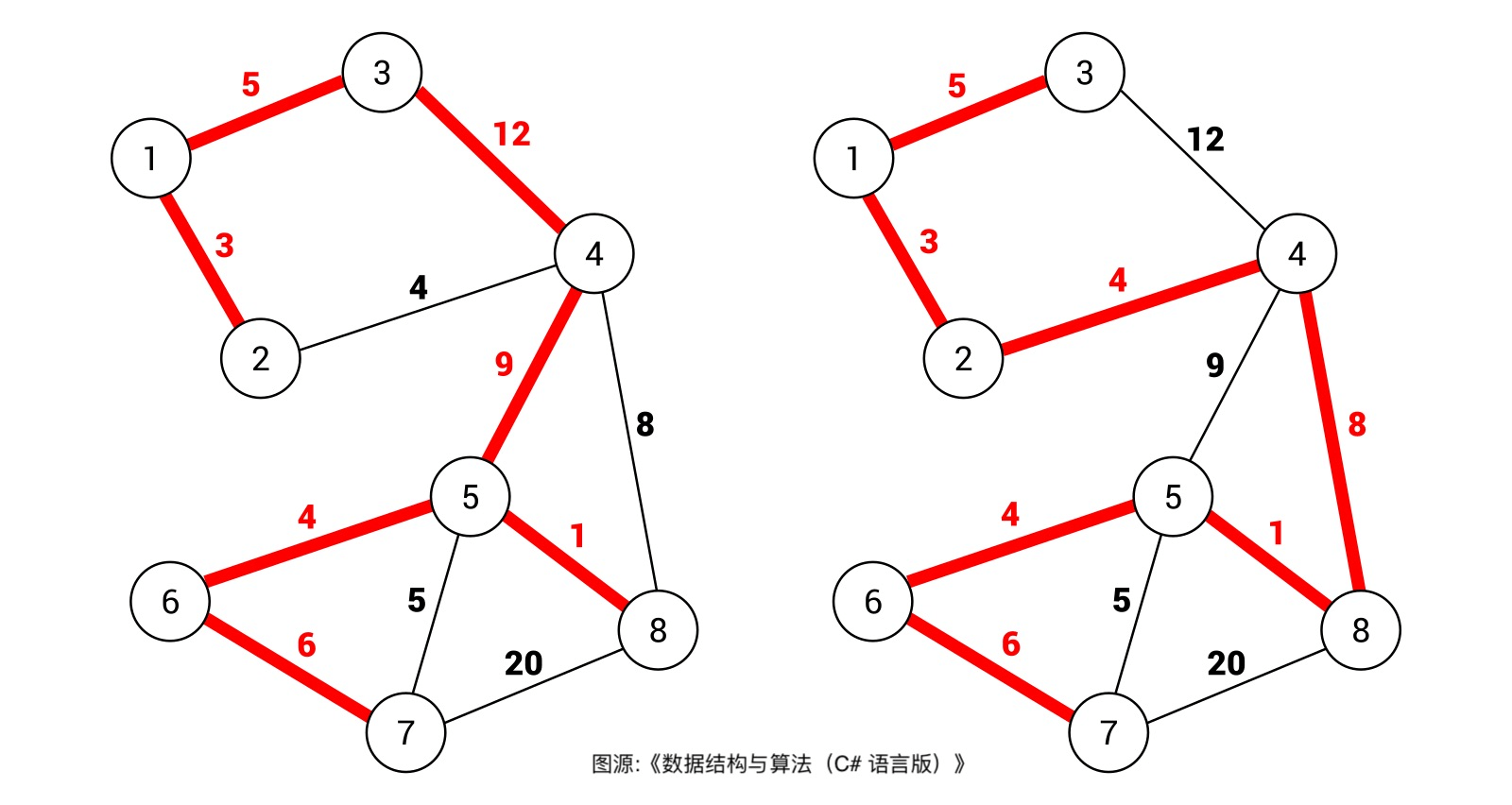
比如下面这幅图，红色的边就组成了两棵不同的生成树

• 最小生成树
  • 所有可能的生成树中，权重和最小的那棵生成树就叫最小生成树
  • 比如上图，右侧生成树的权重和显然比左侧生成树的权重和要小

一般来说，我们都是在无向加权图中计算最小生成树的，所以使用最小生成树算法的现实场景中，图的边权重一般代表成本、距离这样的标量。

图生成树的合法性

更多参考 261. 以图判树：判断图是否可以生成树

Kruskal 算法（克鲁斯卡尔算法）

MST 是 Minimum Spanning Tree 的缩写，中文译为“最小生成树“

所谓==最小生成树==，就是==图中若干边的集合==（ mst，最小生成树的英文缩写），你要保证这些边：

1. 包含图中的所有节点
2. 形成的结构是树结构（即不存在环）
3. 权重和最小

• 前两条就是 261. 以图判树：判断图是否可以生成树 这题实现的功能
• 关键在于第 3 点，如何保证生成树权重和最小

这里就用到了贪心思路：

• 将所有边按照权重从小到大排序，从权重最小的边开始遍历
  • 如果这条边和 mst 中的其它边不会形成环，则这条边是最小生成树的一部分，将它加入 mst 集合；
  • 否则，这条边不是最小生成树的一部分，不要把它加入 mst 集合。

这样，最后 mst 集合中的边就形成了最小生成树

下面我们看两道例题来运用一下 ==Kruskal 算法==

例题一：最低成本连通所有城市

1135. 最低成本连通所有城市

例题二：