根据前序和后序遍历构造二叉树
根据后序构建
mapping,而另外两个都是根据中序构建mapping
同样的思路:
- 找根节点:
- 前序的第一元素 或 后序的最后一个元素
- 构造左、右子树
- 前序的
第二个元素作为左子树的根 - 后序中寻找左子树根节点的值
- 从而确定了
左子树的索引边界- 进而确定
右子树的索引边界,递归构造左右子树
- 进而确定
- 从而确定了
- 前序的
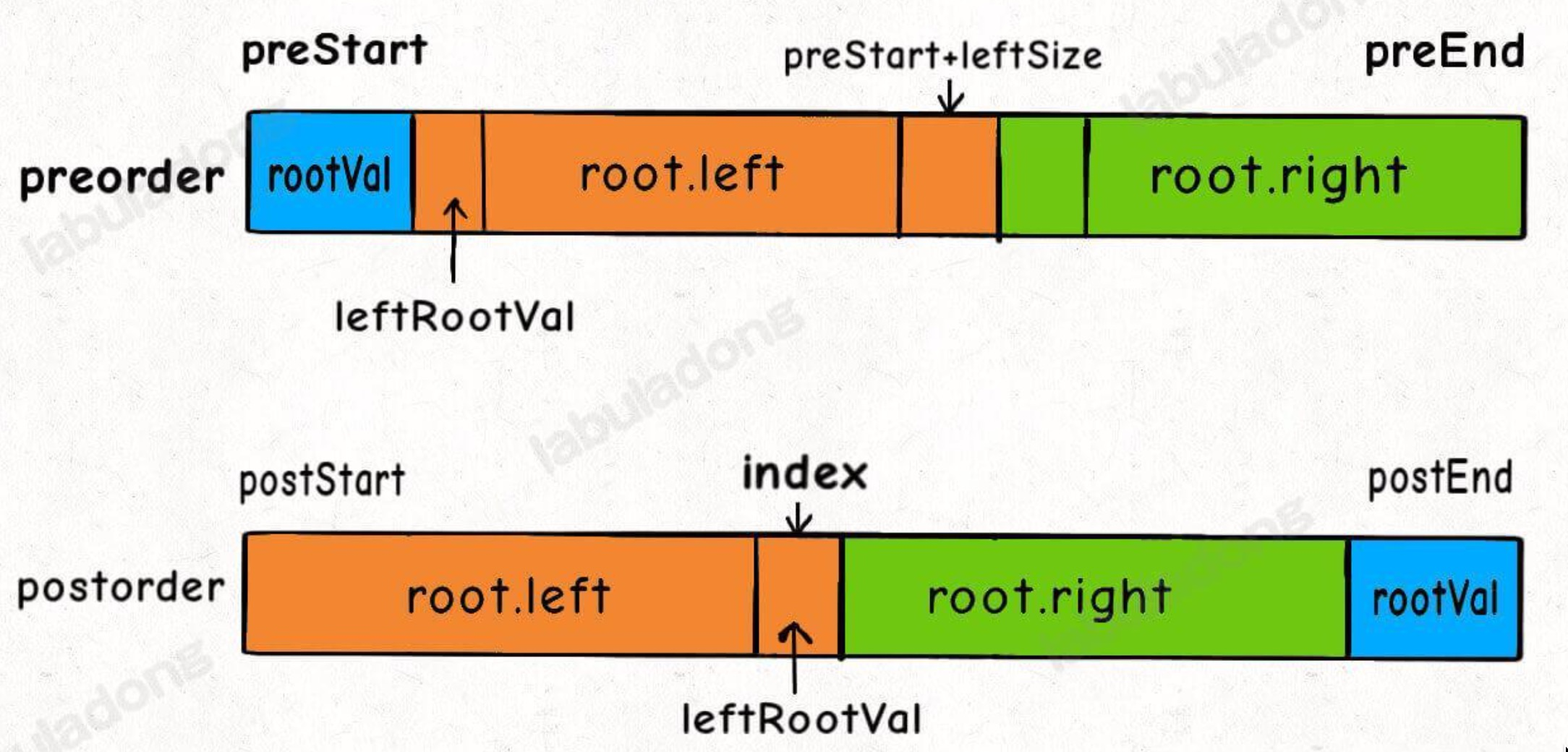
如下图
目录
1. 代码
var constructFromPrePost = function (preorder, postorder) {
let n = preorder.length;
let mapping = {};
postorder.forEach((item, index) => {
mapping[item] = index;
});
return build(0, n - 1, 0, n - 1);
function build(preStart, preEnd, postStart, postEnd) {
// 基础情况
if (preStart > preEnd) return null;
// 处理只有一个节点的情况
if (preStart === preEnd) {
return new TreeNode(preorder[preStart]);
}
// 构造根节点
let rootVal = preorder[preStart];
// 左子树的根节点值
let leftRootVal = preorder[preStart + 1];
// 在后序中找到左子树根节点的位置
let leftRootIndex = mapping[leftRootVal];
// 计算左子树的大小
let leftSize = leftRootIndex - postStart + 1;
// 构造根节点
let root = new TreeNode(rootVal);
// 递归构造左子树
root.left = build(
preStart + 1, // 左子树在前序中的起始位置
preStart + leftSize, // 左子树在前序中的结束位置
postStart, // 左子树在后序中的起始位置
leftRootIndex, // 左子树在后序中的结束位置
);
// 递归构造右子树
root.right = build(
preStart + leftSize + 1, // 右子树在前序中的起始位置
preEnd, // 右子树在前序中的结束位置
leftRootIndex + 1, // 右子树在后序中的起始位置
postEnd - 1, // 右子树在后序中的结束位置
);
return root;
}
};
2. 为什么不唯一?
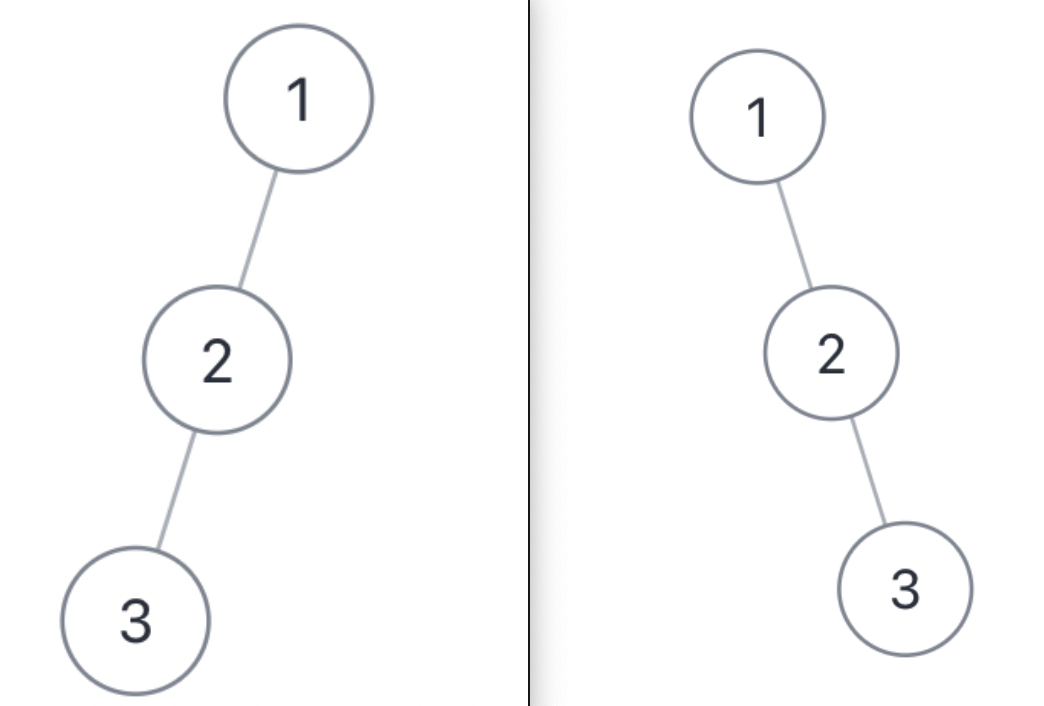
上面两棵树结构不同,但是它们的前序遍历和后序遍历结果是相同的
前序和后序遍历构造二叉树结果不唯一,是因为无法确定空节点的位置
- 前序遍历:根 -> 左 -> 右
- 后序遍历:左 -> 右 -> 根
- 当一个节点只有一个子节点时,仅通过前序和后序遍历,无法确定这个子节点是左子节点还是右子节点
- 而中序遍历可以帮助确定这一点(因为中序遍历是 左 -> 根 -> 右)
示例: