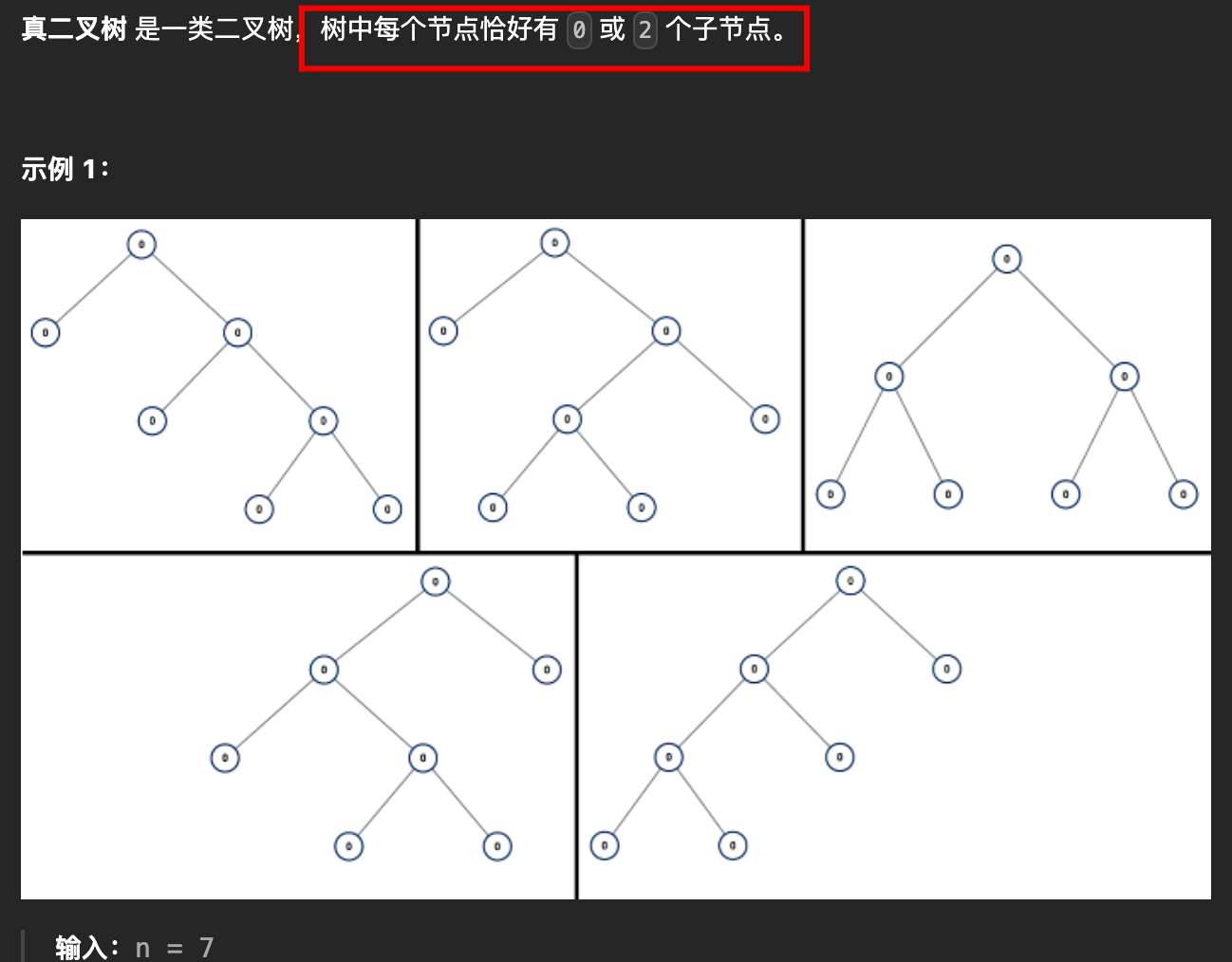
所有可能的真二叉树：节点数为 n 的所有满二叉树

894. 所有可能的真二叉树

关键点：for (let i = 1; i < n; i = i + 2) {

1. 为什么从 1 开始？
   • i 代表左子树的节点个数
   • 最少需要1个节点（不能为0，因为真二叉树的节点度只能是0或2）
2. 为什么小于n？
   • 因为 i 是左子树的节点数
   • 还需要预留一个节点作为根节点
   • 还需要至少一个节点给右子树
   • 所以 i 必须小于总节点数 n
3. 为什么i+2？
   • 因为真二叉树的节点总数必须是奇数
   • 左子树作为一个独立的真二叉树，其节点数也必须是奇数
   • 所以每次增加 2 来保证只遍历奇数

var allPossibleFBT = function (n) {
    let memo = new Array(n + 1).fill(null);
    // 满二叉树不可能是偶数个节点
    if (n % 2 === 0) return [];
    return build(n);
    // 生成节点树为 n 的所有可能的满二叉树，返回 res
    function build(n) {
        let res = [];
        if (n === 1) {
            res.push(new TreeNode(0));
            return res;
        }
        if (memo[n]) return memo[n];
        for (let i = 1; i < n; i = i + 2) {
            // 递归生成所有可能的左子树
            let left = build(i);
            // 递归生成所有可能的右子树
            // 右子树节点数 = 总节点数 - 根节点 - 左子树节点数
            let right = build(n - i - 1);
            // 左右子树的不同排列也能构成不同的二叉树
            for (let L of left) {
                for (let R of right) {
                    let root = new TreeNode(0);
                    root.left = L;
                    root.right = R;
                    res.push(root);
                }
            }
        }
        memo[n] = res;
        return res;
    }
};