图的 DFS 遍历

#算法 #算法/图 #DFS #BFS

1. 总结

图的遍历还是多叉树的延伸，只不过多了一个 visited 数组
遍历图的所有 ==路径==
- 需要 onPath 数组在前序位置标记节点，在后序位置撤销标记

路径 → 回溯算法

图的遍历就是==多叉树的遍历的延伸==
- 主要的遍历方式还是 DFS 和 BFS
- 唯一的区别是，==树结构中不存在环，而图结构中可能存在环==，
  - 所以需要==标记遍历过的节点==，避免遍历函数在环中死循环。
    - 遍历图的所有「节点」时，需要 visited 数组在==前序位置标记节点==
    - 如果题目说这幅图不存在环，那么图的遍历就完全等同于多叉树的遍历

2. DFS 遍历

2.1. 遍历图的所有==节点==：使用 `visited`

[!info]

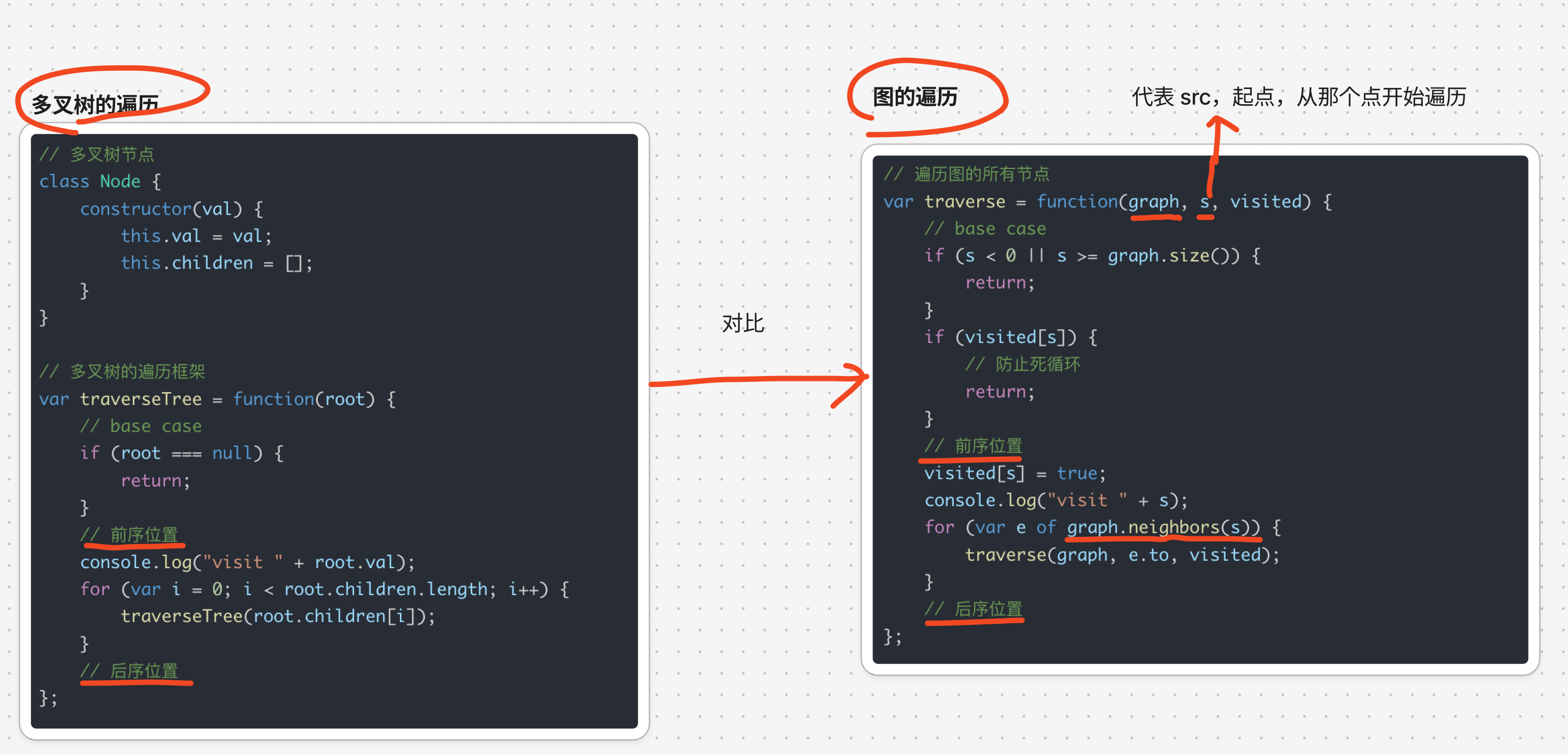
对比多叉树的遍历，很快能理解，如下

区别在于多了两个参数 src 和 visited

2.1.1. 多叉树 → 图的 DFS

cos-blog-832-34-20241012

2.1.2. 复杂度分析

为什么图的深度优先搜索（DFS）遍历的时间复杂度是 O(E + V)，其中 E 是边的数量，V 是顶点的数量。

遍历所有顶点：O(V)
- 在 DFS 中，我们需要访问每个顶点至少一次。
探索所有边：O(E)
- 对于每个顶点，我们需要探索与之相连的所有边。
- 在整个过程中，每条边最多被考虑两次（对于无向图）或一次（对于有向图）
- 因此，探索所有边需要 O(E) 的时间。
合并复杂度
- 将这两部分组合起来，我们得到总的时间复杂度为 O(V + E)。
对于邻接表表示的图
- 访问每个顶点：O(V)
- 对于每个顶点，我们遍历其邻接列表。
  - 所有邻接列表的总长度等于边的数量（对于无向图是2E，对于有向图是E）
  - 因此，遍历所有邻接列表的总时间是 O(E)。
对于邻接矩阵表示的图
- 访问每个顶点：O(V)
- 对于每个顶点，我们需要检查它与所有其他顶点是否相连，这需要 O(V) 时间。
- 总的时间复杂度是 O(V^2)，但是我们通常表示为 O(V + E)，因为在最坏的情况下（完全图），E = V^2

2.1.3. 为什么不是 `O(V * E)`？

因为我们似乎对每个顶点都要检查所有边。实际上，DFS 不会对每个顶点都检查所有边。

每条边只会被检查有限次（通常是一次或两次），而不是 V 次

因为有 visited 数组

2.1.4. 多叉树的复杂度为什么是 `O(N)`，不算边的数量？

其实二叉树/多叉树的遍历函数，也要算上边的数量，只不过对于树结构来说，边的数量和节点的数量是近似相等的
所以时间复杂度还是 O(N + N) = O(N)。

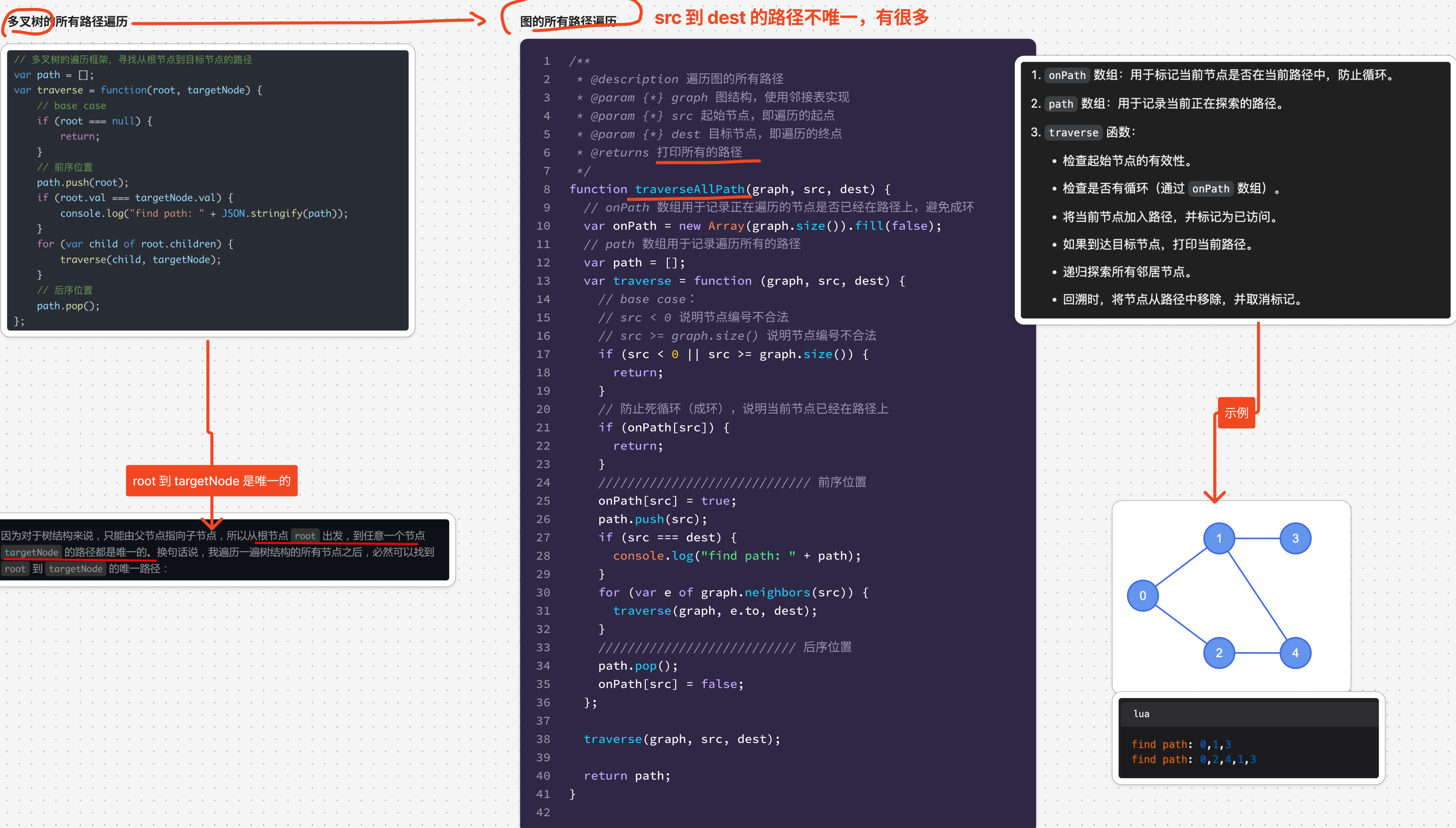
2.2. 遍历所有的==路径==：使用 onPath

多叉树的路径遍历 → 图的路径遍历

cos-blog-832-34-20241012|1264

/**
 * @description 遍历图的所有路径
 * @param {*} graph 图结构，使用邻接表实现
 * @param {*} src 起始节点，即遍历的起点
 * @param {*} dest 目标节点，即遍历的终点
 * @returns 打印所有的路径
 */
function traverseAllPath(graph, src, dest) {
  // onPath 数组用于记录正在遍历的节点是否已经在路径上，避免成环
  var onPath = new Array(graph.size()).fill(false);
  // path 数组用于记录遍历所有的路径
  var path = [];
  var traverse = function (graph, src, dest) {
    // base case：
    // src < 0 说明节点编号不合法
    // src >= graph.size() 说明节点编号不合法
    if (src < 0 || src >= graph.size()) {
      return;
    }
    // 防止死循环（成环），说明当前节点已经在路径上
    if (onPath[src]) {
      return;
    }
    // 前序位置:更新 onpath 和 src
    onPath[src] = true;
    path.push(src);
    if (src === dest) {
      console.log("find path: " + path);
    }
    for (var e of graph.neighbors(src)) {
      traverse(graph, e.to, dest);
    }
    // 后序位置:回溯
    path.pop();
    onPath[src] = false;
  };

  traverse(graph, src, dest);

  return path;
}

2.3. 剪枝：同时利用 `visited` 和 `onPath`

后面有习题需要同时利用 visited 和 onPath 数组来进行剪枝优化复杂度

4. 参考

https://labuladong.online/algo/data-structure-basic/graph-traverse-basic/

liguwe's site