列队:Python 描述
#列队 #算法/列队 #数据结构/列队 #环形数组
目录
1. 定义
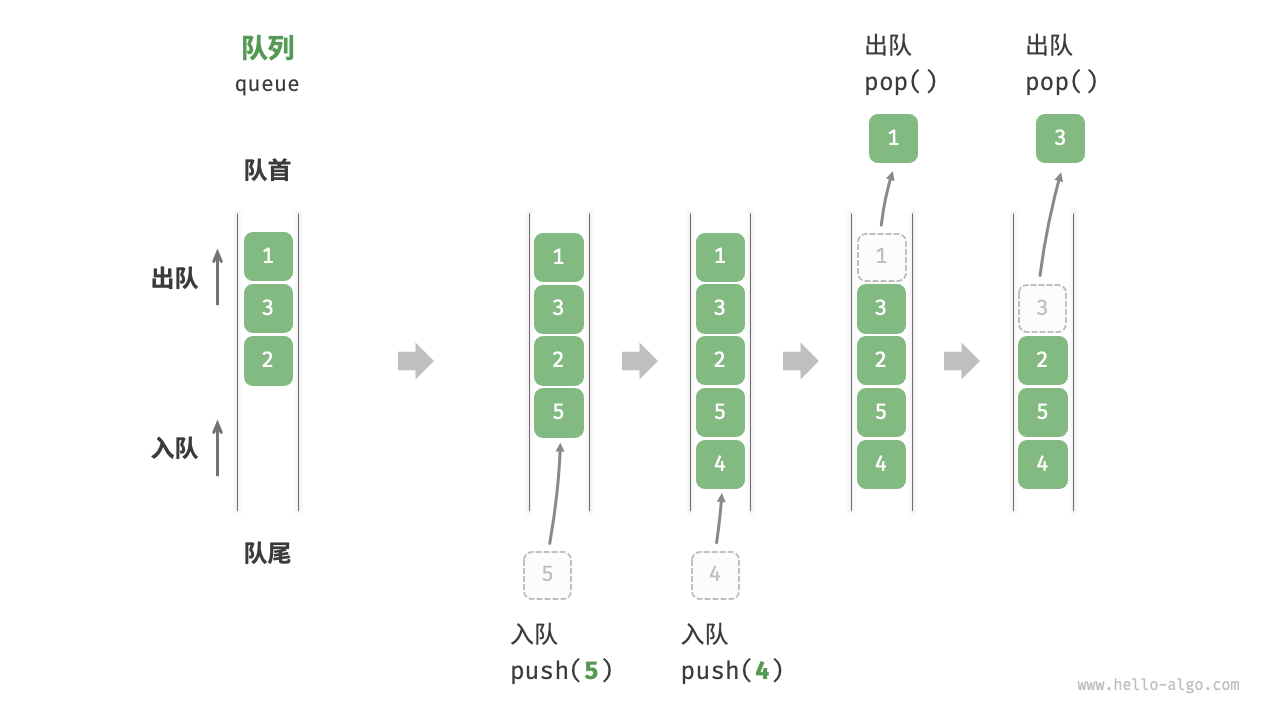
2. 列队的常用操作
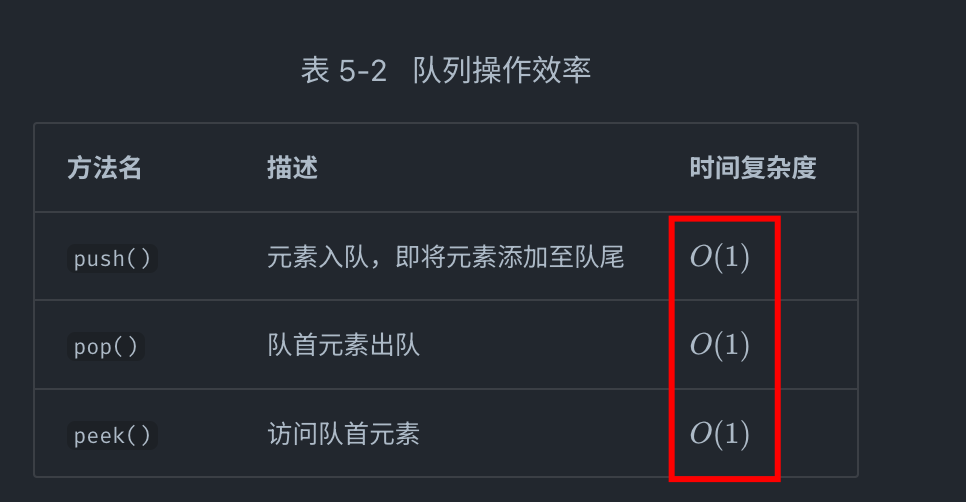
JavaScript 的入队操作是是
push,出队操作是shift
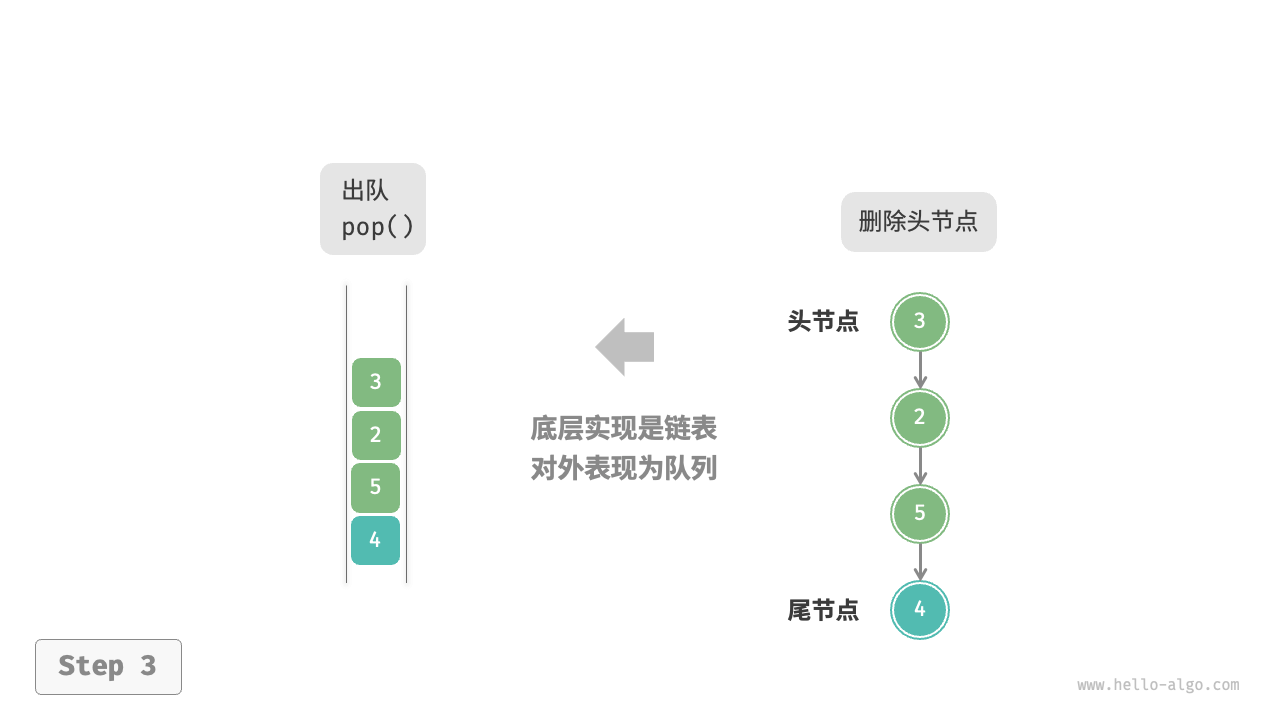
3. 基于链表的实现
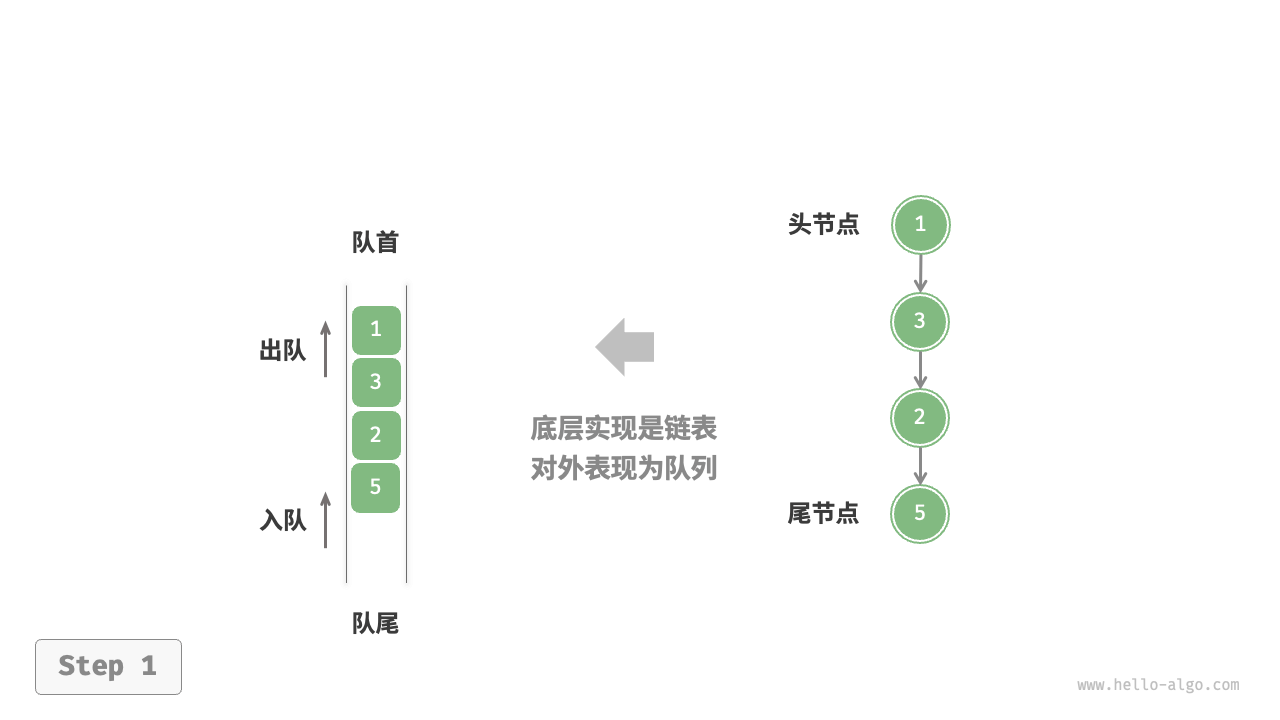
入队
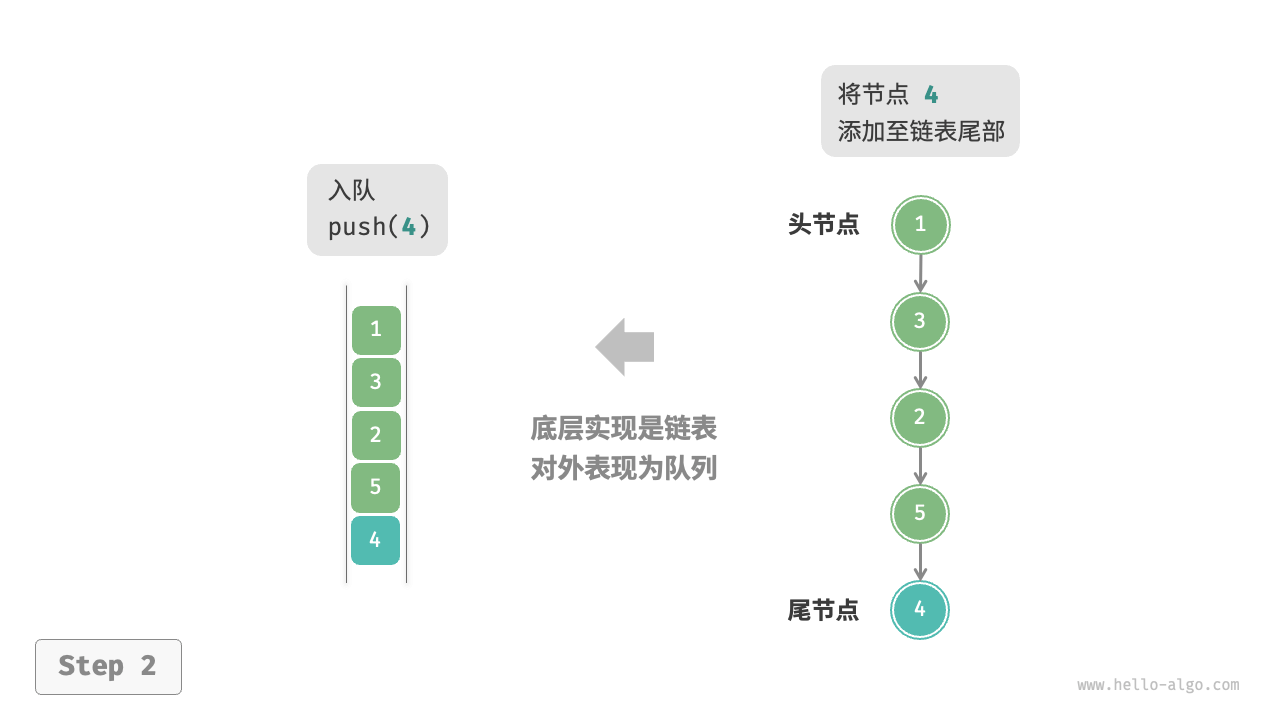
出队
3.1. 完全实现
"""节点类: 用于构造链表节点"""
class ListNode:
def __init__(self,val:int) -> None:
# 节点值
self.val = val
# listNode | Node 代表 self.next 的值可能是 listNode | Node
self.next:ListNode | None = None
# 基于链表的队列
class linkedQueue:
def __init__(self):
# 队列的头
self.head = None
# 队列的大小
self.sz = 1
# 返回队列的大小
def size(self):
return self.sz
# 判断队列是否为空
def isEmpty(self):
return self.sz == 0
# 入队
def enqueue(self, val):
# 创建一个新节点
node = ListNode(val)
# 如果队列为空
if self.head is None:
self.head = node
# 如果队列不为空
else:
# 将新节点插入到队列的尾部 【底部】
p = self.head
while p.next is not None:
p = p.next
p.next = node
self.sz += 1
# 出队
def dequeue(self):
if self.isEmpty():
raise Exception("queue is empty")
# 保存队头元素
item = self.head
# 删除队头元素
# 直接将 head 指向下一个元素即可
# 但是要注意,如果 head 是 None,就不需要再指向下一个元素了
# 因为 head 是 None 说明队列为空,没有下一个元素了
# 所以这里需要判断一下 head 是否是 None
if self.head is not None:
self.head = self.head.next
self.sz -= 1
return item
# 返回队头元素
def peek(self):
if self.isEmpty():
raise Exception("queue is empty")
return self.head
3.2. 基于 deque 的实现
from collections import deque
# 用链表作为底层数据结构实现队列
# Python 的 deque 就是双链表
class MyLinkedQueue:
def __init__(self):
self.list = deque()
# 向队尾插入元素,时间复杂度 O(1)
def enqueue(self, e):
self.list.append(e)
# 从队头删除元素,时间复杂度 O(1)
def dequeue(self):
# 使用双端队列的 popleft 方法
# 即从队头删除元素
# popleft 代表从左边删除元素
return self.list.popleft()
# 查看队头元素,时间复杂度 O(1)
def peek(self):
return self.list[0]
# 返回队列中的元素个数,时间复杂度 O(1)
def size(self):
return len(self.list)
4. 基于数组的实现
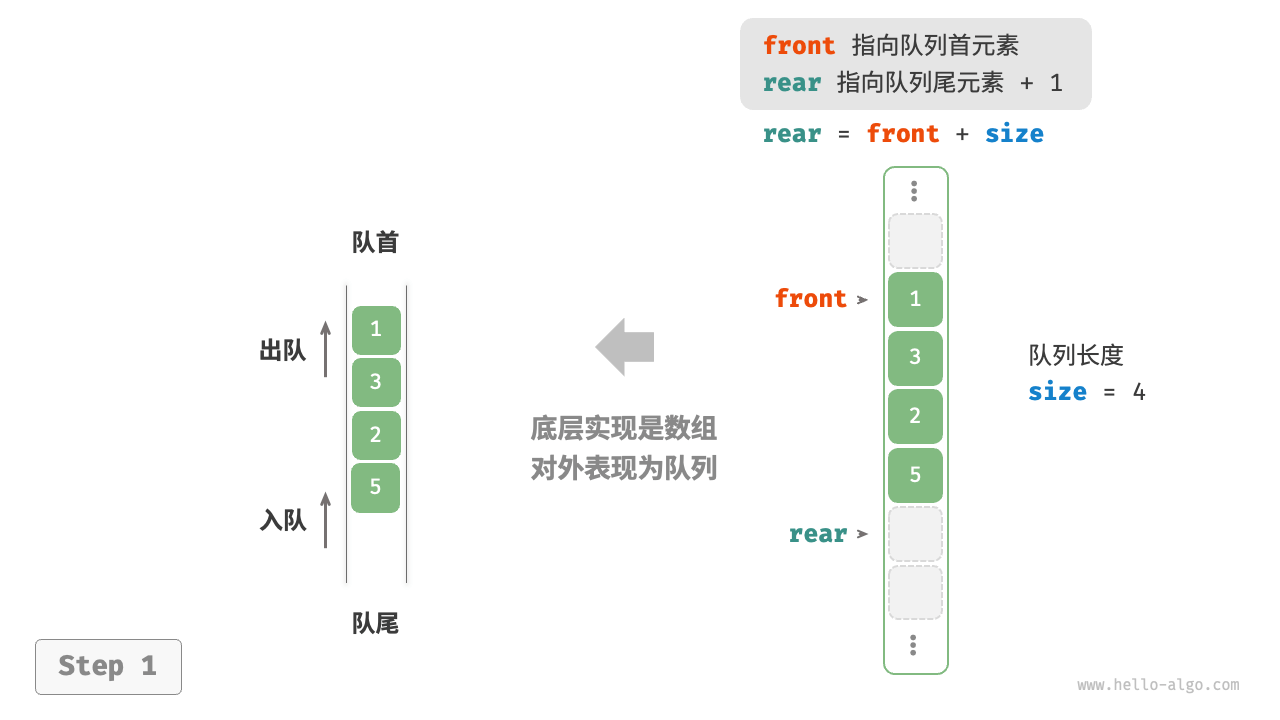
4.1. 先看下环形数组技巧
[!danger] 环形数组技巧利用求模(余数)运算,将普通数组变成逻辑上的环形数组,可以让我们用
O(1)的时间在数组头部增删元素
先看个示例,把数组循环打印
arr = [1, 2, 3, 4, 5]
# 循环打印列表,当打印完成后,继续打印列表,一直循环
i = 0
while i < len(arr):
print(arr[i])
# 当 i 等于列表的最后一个元素时,将 i 设置为 0
# 求模运算 %,也就是求余数
# 当 i 到达数组末尾元素时,i + 1 和 arr.length 取余数又会变成 0,即会回到数组头部
# 这样就在逻辑上形成了一个环形数组,永远遍历不完
i = (i + 1) % len(arr)
4.1.1. 比较复杂的版本:考虑扩容等
[!danger] 知道就行,没必要,Python 内置的很多内容足够用了,不需要实现
[start, end)注意区间
class CycleArray:
def __init__(self, size: int) -> None:
# 数组容量
self.capacity = size
# 数组,初始化为 None
self.arr = [None] * size
# start 指针 指向第一个有效元素的索引
self.start = 0
# end 指针 指向最后一个有效元素的下一个位置索引
self.end = 0
self.count = 0
def resize(self, newSize):
# 创建新数组
new_arr = [None] * newSize
# 将原数组的元素复制到新数组
for i in range(self.count):
new_arr[i] = self.arr[(self.start + i) % self.capacity]
# 更新数组
self.arr = new_arr
# 更新 start 指针
self.start = 0
# 更新 end 指针
self.end = self.count
# 更新容量
self.capacity = newSize
# 在队头添加元素
def add_first(self, val):
# 如果队列已满,扩容 2 倍
if self.is_full():
self.resize(self.capacity * 2)
# 因为 start 是闭区间,所以先左移,再赋值
self.start = (self.start - 1 + self.capacity) % self.capacity
self.arr[self.start] = val
self.count += 1
# 删除队头元素
def remove_first(self):
if self.is_empty():
raise Exception("Array is empty")
self.arr[self.start] = None
self.start = (self.start + 1) % self.capacity
self.count -= 1
if self.count > 0 and self.count == self.capacity // 4:
self.resize(self.capacity // 2)
def add_last(self, val):
if self.is_full():
self.resize(self.capacity * 2)
self.arr[self.end] = val
self.end = (self.end + 1) % self.capacity
self.count += 1
def remove_last(self):
if self.is_empty():
raise Exception("Array is empty")
self.end = (self.end - 1 + self.capacity) % self.capacity
self.arr[self.end] = None
self.count -= 1
if self.count > 0 and self.count == self.capacity // 4:
self.resize(self.capacity // 2)
def get_first(self):
if self.is_empty():
raise Exception("Array is empty")
return self.arr[self.start]
def get_last(self):
if self.is_empty():
raise Exception("Array is empty")
return self.arr[(self.end - 1 + self.capacity) % self.capacity]
def is_full(self):
return self.count == self.capacity
def size(self):
return self.count
def is_empty(self):
return self.count == 0
4.1.2. 使用 deque:最好的方式
from collections import deque
# 创建一个最大长度为 5 的环形数组
circular_array = deque(maxlen=5)
# 添加元素
for i in range(7):
circular_array.append(i)
print(f"After appending {i}: {list(circular_array)}")
# 输出:
# After appending 0: [0]
# After appending 1: [0, 1]
# After appending 2: [0, 1, 2]
# After appending 3: [0, 1, 2, 3]
# After appending 4: [0, 1, 2, 3, 4]
# After appending 5: [1, 2, 3, 4, 5]
# After appending 6: [2, 3, 4, 5, 6]
# 从左侧添加元素
circular_array.appendleft(10)
print(f"After appendleft 10: {list(circular_array)}")
# 输出:After appendleft 10: [10, 2, 3, 4, 5]
4.2. 使用 deque 实现列队:最佳方案
from collections import deque
# 用deque 来实现队列
class MyQueue:
def __init__(self):
self.list = deque()
# 向队尾插入元素,时间复杂度 O(1)
def enqueue(self, e):
self.list.append(e)
# 从队头删除元素,时间复杂度 O(1)
def dequeue(self):
return self.list.popleft()
# 查看队头元素,时间复杂度 O(1)
def peek(self):
return self.list[0]
# 返回队列中的元素个数,时间复杂度 O(1)
def size(self):
return len(self.list)
5. 再看下环形数组
5.1. 实现方式
- 对于大多数情况,
collections.deque是最佳选择,因为它是 Python 标准库的一部分,性能好,使用简单。 - 如果你需要更多的控制或者想要理解环形数组的工作原理,可以自己实现一个简单的版本。
- 对于特殊需求,比如需要进行大量数值计算,可以考虑使用 NumPy。
- 如果需要更专门的环形缓冲区实现,可以考虑使用第三方库如 CircularBuffer。
5.2. 使用场景
- 缓冲区管理
- 音频和视频流处理:在处理连续的音频或视频数据时,环形缓冲区可以用来存储最近的一段数据,便于回放或处理。
- 网络数据包处理:网络设备可以使用环形缓冲区来临时存储接收到的数据包,等待处理。
- 任务调度
- 操作系统的进程调度:操作系统可以使用环形数组来实现轮转调度算法,循环分配CPU时间给不同的进程。
- 定时任务管理:在需要周期性执行任务的系统中,环形数组可以用来管理这些任务的执行顺序。
- 数据流处理
- 滑动窗口算法:在处理时间序列数据时,环形数组可以高效地实现滑动窗口,用于计算移动平均等指标。
- 实时数据分析:保存最近N个数据点进行实时分析和统计。
- 游戏开发
- 回放功能:在游戏中实现最近N秒的即时回放功能。
- 循环地图:一些2D游戏中的无限循环地图可以用环形数组来实现。
- 内存管理
- 内存分配器:某些内存分配算法使用环形数组来管理内存块。
- 通信系统
- 消息队列:在生产者-消费者模型中,环形缓冲区可以用作消息队列。
- 历史记录管理
- 命令历史:保存用户最近执行的N个命令,以便快速访问。
- 浏览器历史:管理浏览器的前进/后退功能。
- 数据压缩
- LZ77等压缩算法:在某些数据压缩算法中,环形缓冲区用于存储最近处理过的数据。
- 实时系统
- 传感器数据处理:在实时系统中,环形缓冲区可以用于存储和处理来自传感器的连续数据流。
- 数据库系统
- 日志管理:某些数据库系统使用环形缓冲区来管理事务日志。
6. 列队的使用场景
- 任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序。
- 又比如购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单