单调列队算法

#leetcode #算法/单调列队 #算法/数据结构算法

第 239 题「滑动窗口最大值」

目录

• 1. 定义
• 2. 用途
• 3. 单调递减队列的实现
  • 3.1. push(item) 的逻辑
  • 3.2. pop(item) 的逻辑

1. 定义

队列中的元素全都是单调递增（或递减）的

2. 用途

• 它可以快速确定滑动窗口中的最大或最小值
  • 单调队列结合滑动窗口方法可以在O(1)时间内计算当前窗口中的最大值或最小值
  • 同时保持队列先进先出的特性

3. 单调递减队列的实现

先看看 普通的队列的标准 API

// 普通的队列的标准 API
class Queue {
  // enqueue 操作，在队尾加入元素 n
  push(n) {}

  // dequeue 操作，删除队头元素
  pop() {}
}

单调递减队列的标准 API

// 单调递减队列的标准 API
class MonotonicQueue {
  // 在队尾添加元素 n
  push(n) {}

  // 返回队头元素
  max() {}

  // 删除队头元素
  pop() {}
}

下面是具体实现

// 单调递增队列的标准 API
class MonotonicQueue {
  constructor() {
    // 维护其中的元素自尾部到头部单调递增
    this.maxq = [];
  }

  // 在队尾添加元素 item
  // 在尾部添加一个元素 item，维护 maxq 的单调性质
  // 将前面小于自己的元素都删
  push(item) {
    // 将前面小于自己的元素都删除
    while (this.maxq.length > 0 && this.maxq[this.maxq.length - 1] < item) {
      // 删除数组的最后一个元素
      this.maxq.pop();
    }
    this.maxq.push(item);
  }

  // 返回队头元素, 即 maxq 队首元素
  // 队头的元素肯定是最大的
  max() {
    return this.maxq[0];
  }

  // 删除队头元素,
  pop(item) {
    // 如果要删除的元素是队头元素，就删除
    // 否则不做任何操作
    // 想删除的队头元素 item 可能已经被「压扁」了
    if (this.maxq[0] === item) {
      // 删除数组的第一个元素
      this.maxq.shift();
    }
  }
}

3.1. push(item) 的逻辑

关于 push(item) 的逻辑，可以参考下图

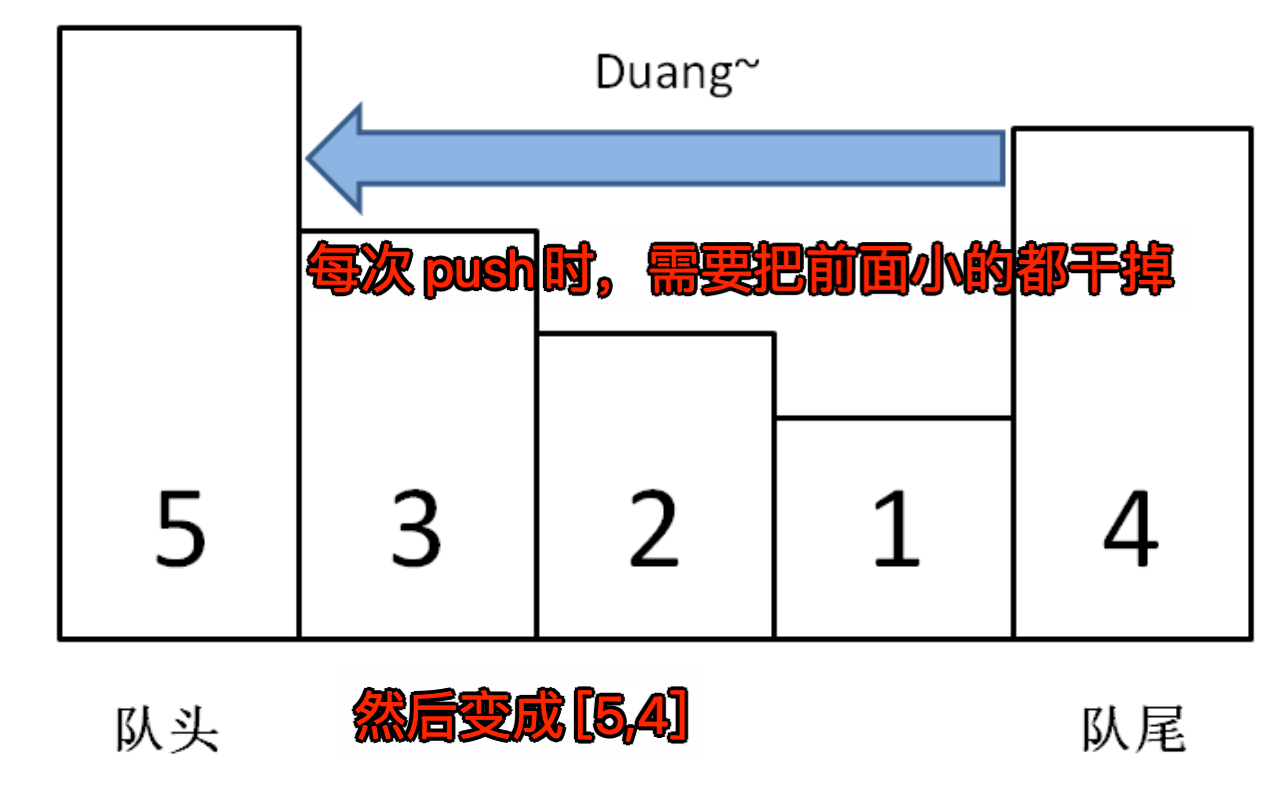
[!danger] 会有疑问❓，都 pop 删除了，那岂不是队列里没值了，不是因为每次都会 push ，长度都会+1 ，即使把前面的元素都干掉了，长度还是持续增加

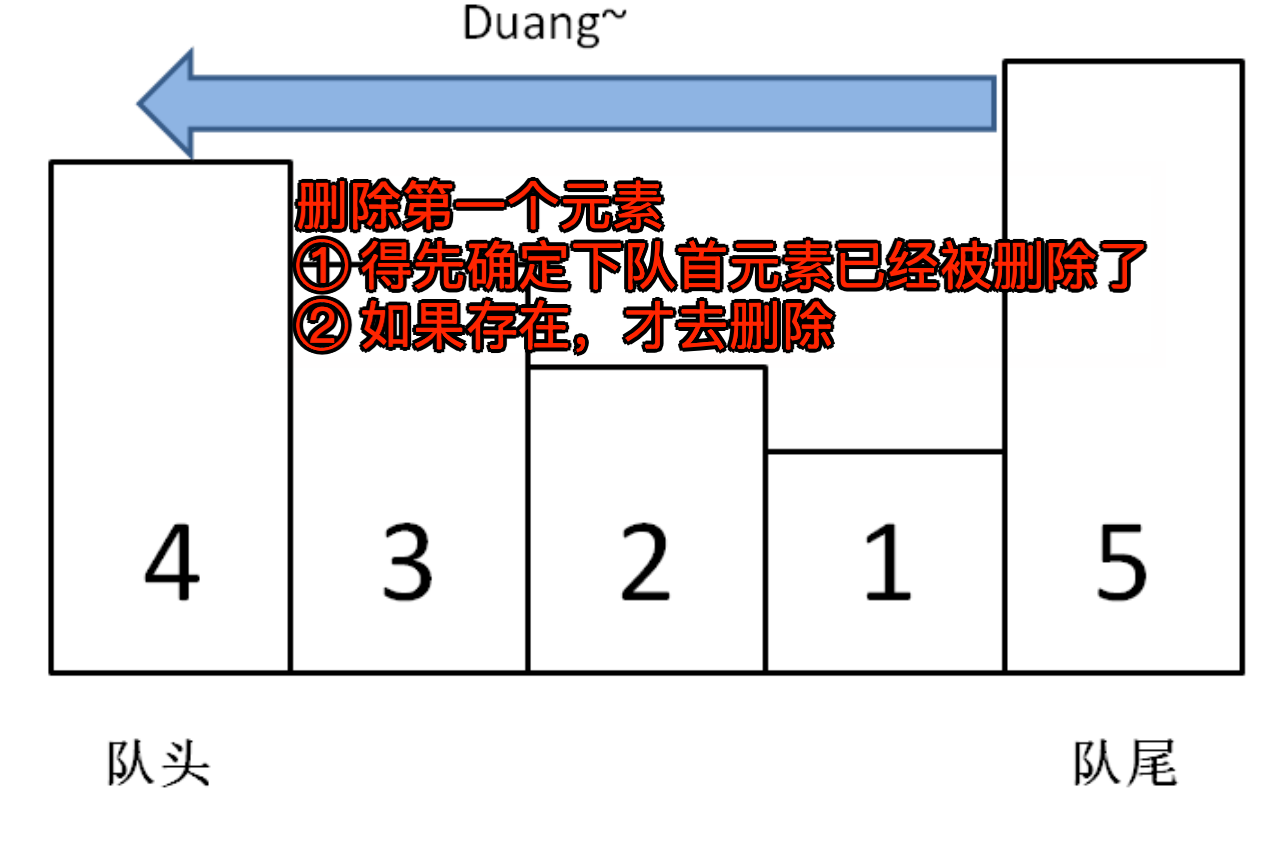
3.2. pop(item) 的逻辑

删除队首，需要传一个参数，如果它是队首元素才需要删除