所有可能的路径

797. 所有可能的路径

目录

1. 总结

  • 分别使用 dfs(traverse) 和 backtrack 两种方法实现，需要注意这两种方法的区别
    • 关注节点还是路径
    • 选择和撤销选择是在 for 循环的外面还是里面
  • 最后都需要关注 dfs(traverse) 和 backtrack 的==三个入参==
    • 邻接表
    • 从哪个顶点开发遍历：src
    • 路径：path

2. 题目

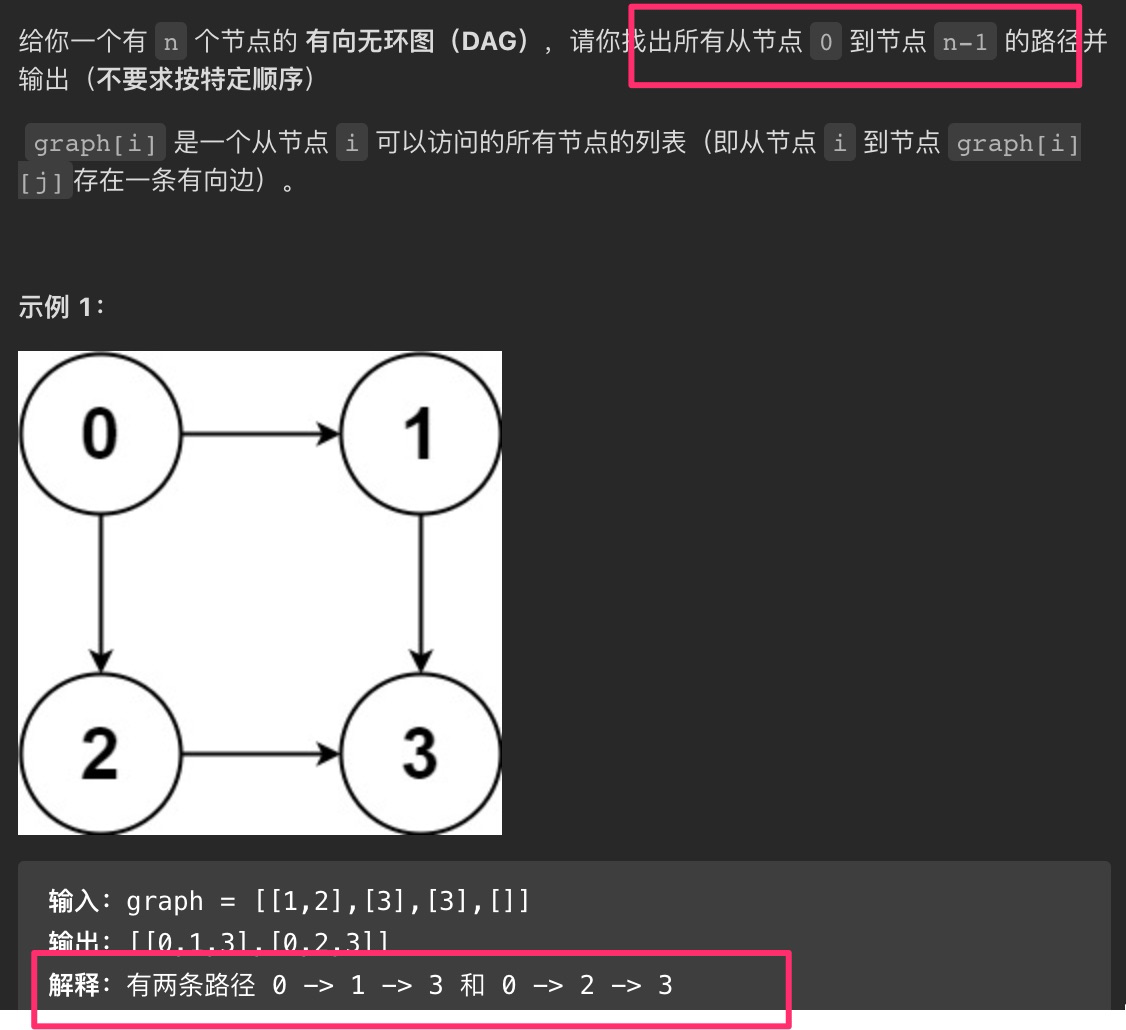
看力扣第 797 题「 所有可能路径」, image.png|456 image.png|568

3. 分析

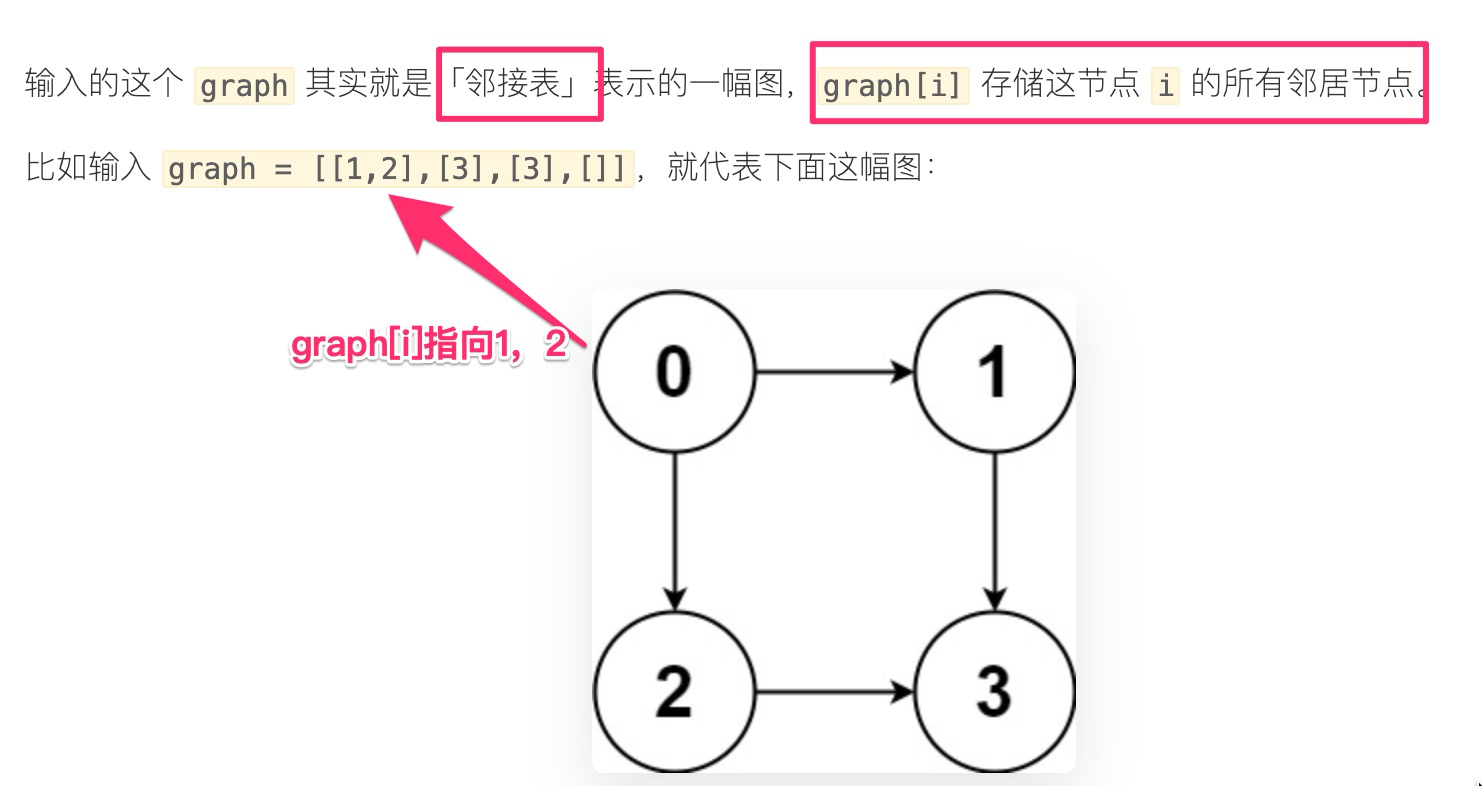
  • 以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可
  • 既然输入的图是无环的，我们就不需要 visited 数组辅助了，直接套用图的遍历框架：

4. DFS 解法

DFS 关注节点，关于 DFS 和回溯算法的区别请见 1. 回溯算法与DFS算法的区别

  • 变量名 dfs 或者 traverse 本质都是遍历，可以任意用一个
  • function traverse(graph, src, path) {
    • 参数很重要：
      • 参数 1：邻接表
      • 参数 2：现在从哪个顶点开始遍历
      • 参数 3：==当前的路径==
  • ==顶点都是从 0 → n-1==
  • 因为是 DFS，所以
    • 选择节点和撤销节点都是在外面
    • 在 for 循环的==外面==
/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
const allPathsSourceTarget = function (graph) {
  let res = [];
  let n = graph.length;
  function traverse(graph, src, path) {
    path.push(src);
    if (src === n - 1) {
      res.push([...path]);
      path.pop();
      return;
    }
    for (let v of graph[src]) {
      traverse(graph, v, path);
    }
    path.pop();
  }

  traverse(graph, 0, []);

  return res;
};

5. 回溯算法解法

[!danger] ❌ 错误记录 看下面 ==注释行==

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
const allPathsSourceTarget = function (graph) {
  let res = [];
  let len = graph.length;
  function backtrack(src, path) {
    // 修改终止条件：判断是否到达终点(src === len-1)
    // if(path.length === len -1){
    if (src === len - 1) {
      res.push([...path]);
      return;
    }
    for (let v of graph[src]) {
      path.push(v);
      backtrack(v, path);
      path.pop();
    }
  }
  backtrack(0, [0]);
  return res;
};