如何查找状态转移方程：最长递增子序列与俄罗斯套娃

#算法/动态规划

1. 总结

1.1. 最长递增子序列

一张图：
注意：
- 不是累计 ==res++==
- 状态转移方程： dp[i] = Math.max(dp[j] + 1, dp[i]);

var lengthOfLIS = function (nums) {
  let len = nums.length;
  // 以 num[i] 结尾的最长递增子序列为 dp[i]
  let dp = new Array(len).fill(1);
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[j] + 1, dp[i]);
      }
    }
  }
  return Math.max(...dp);
};

1.2. 俄罗斯套娃

宽度 → 升序
- 高度相等时，则 → 降序
- return a[0] !== b[0] ? a[0] - b[0] : b[1] - a[1];
下面的写法超时了，得用另外一种写法

var maxEnvelopes = function (envelopes) {
  envelopes.sort((a, b) => {
    return a[0] !== b[0] ? a[0] - b[0] : b[1] - a[1];
  });

  let height = [];

  for (let item of envelopes) {
    height.push(item[1]);
  }

  return lengthOfLIS(height);

  function lengthOfLIS(nums) {
    let len = nums.length;
    // 以 num[i] 结尾的最长递增子序列为 dp[i]
    let dp = new Array(len).fill(1);
    for (let i = 0; i < len; i++) {
      for (let j = 0; j < i; j++) {
        if (nums[i] > nums[j]) {
          dp[i] = Math.max(dp[j] + 1, dp[i]);
        }
      }
    }
    return Math.max(...dp);
  }
};

2. 题目

LeetCode	力扣	难度
300. Longest Increasing Subsequence	300. 最长递增子序列	🟠
354. Russian Doll Envelopes	354. 俄罗斯套娃信封问题	🔴

3. 最长递增子序列

|648

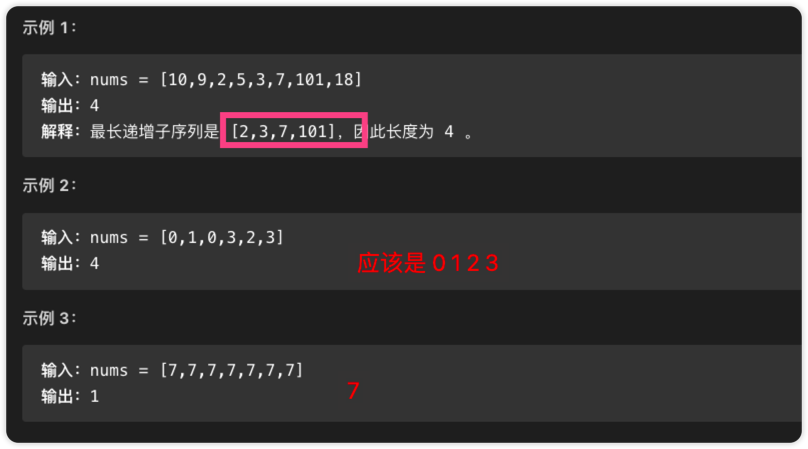
「子序列」和「子串」的区别：

子串一定是连续的
而子序列不一定是连续的

4. 数学归纳法找 `dp数组` 的关系

定义 dp 数组： dp[i]表示以 nums[i]这个数 结尾的最长递增子序列的长度

base case : dp[0] = 1
- 其他的，如下图，关键是需要画出 index , nums , dp 三者的对应关系
- 假设已知 dp[0...4] 需要推导出 => dp[5]
- 先找到所有比 nums[5] 小的，即 nums[0] = 1 和 nums[4] = 2
  - 然后，再比较 dp[0] + 1 和 dp[4] + 1 ，哪个更大？最大值就是 dp[5] 的值

|568

最终代码如下：

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  let len = nums.length;
  // 以 num[i] 结尾的最长递增子序列为 dp[i]
  let dp = new Array(len).fill(1);
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[j] + 1, dp[i]);
      }
    }
  }
  return Math.max(...dp);
};

5. `动态归纳法` 找 `状态转移关系` 的套路总结

1、明确 dp 数组的定义。这一步对于任何动态规划问题都很重要，如果不得当或者不够清晰，会阻碍之后的步骤。

重要非常重要，定义错误就没法往下走了，如果错误，很可能就是 dp 数组的定义不够恰当，需要重新定义 dp 数组的含义；或者可能是 dp 数组存储的信息还不够，不足以推出下一步的答案，需要把 dp 数组扩大成二维数组甚至三维数组

2、根据 dp 数组的定义，运用数学归纳法的思想，假设 dp[0...i-1] 都已知，想办法求出 dp[i]，一旦这一步完成，整个题目基本就解决了

6. `O(NlogN)` 的解法

类似扑克牌，其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关，甚至有一种排序方法就叫做 patience sorting（耐心排序） ，可以利用到二分查找法，具体不展开了，可参考下面链接。

这种解法应用于俄罗斯套娃：二维最长递增子序列，这样才能通过 leetcode 测试

7. 扩展到二维 - 俄罗斯套娃

https://leetcode.cn/problems/russian-doll-envelopes/

|528

解法比较巧妙：

先对宽度 w 进行升序排序，
- 如果遇到 w 相同的情况，则按照高度 h 降序 排序；
之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。

如下图，只需要对 [8,3,4,2,7] 查找 最长递增子序列 即可，不好理解的话看下面两张图

|480

如下图，最长递增子序列 [3 4 7]

|374

具体代码如下：

/**
 * @param {number[][]} envelopes
 * @return {number}
 */
function maxEnvelopes(envelopes) {
    let n = envelopes.length;
    // 按宽度升序排列，如果宽度一样，则按高度降序排列
    envelopes.sort((a, b) => {
        return a[0] === b[0] ?
            b[1] - a[1] : a[0] - b[0];
    });
    // 对高度数组寻找 LIS
    let height = new Array(n);
    for (let i = 0; i < n; i++) {
        height[i] = envelopes[i][1];
    }
    return lengthOfLIS(height);
}

function lengthOfLIS(nums) {
    // dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
    // base case：dp 数组全都初始化为 1
    let dp = new Array(nums.length).fill(1);
    for (let i = 0; i < nums.length; i++) {
        for (let j = 0; j < i; j++) {
            if (nums[i] > nums[j])
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
    let res = 0;
    for (let i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

[!danger] 注意：以上方式不能通过 LeetCode 的所有用例，需要使用二分法才能通过

liguwe's site