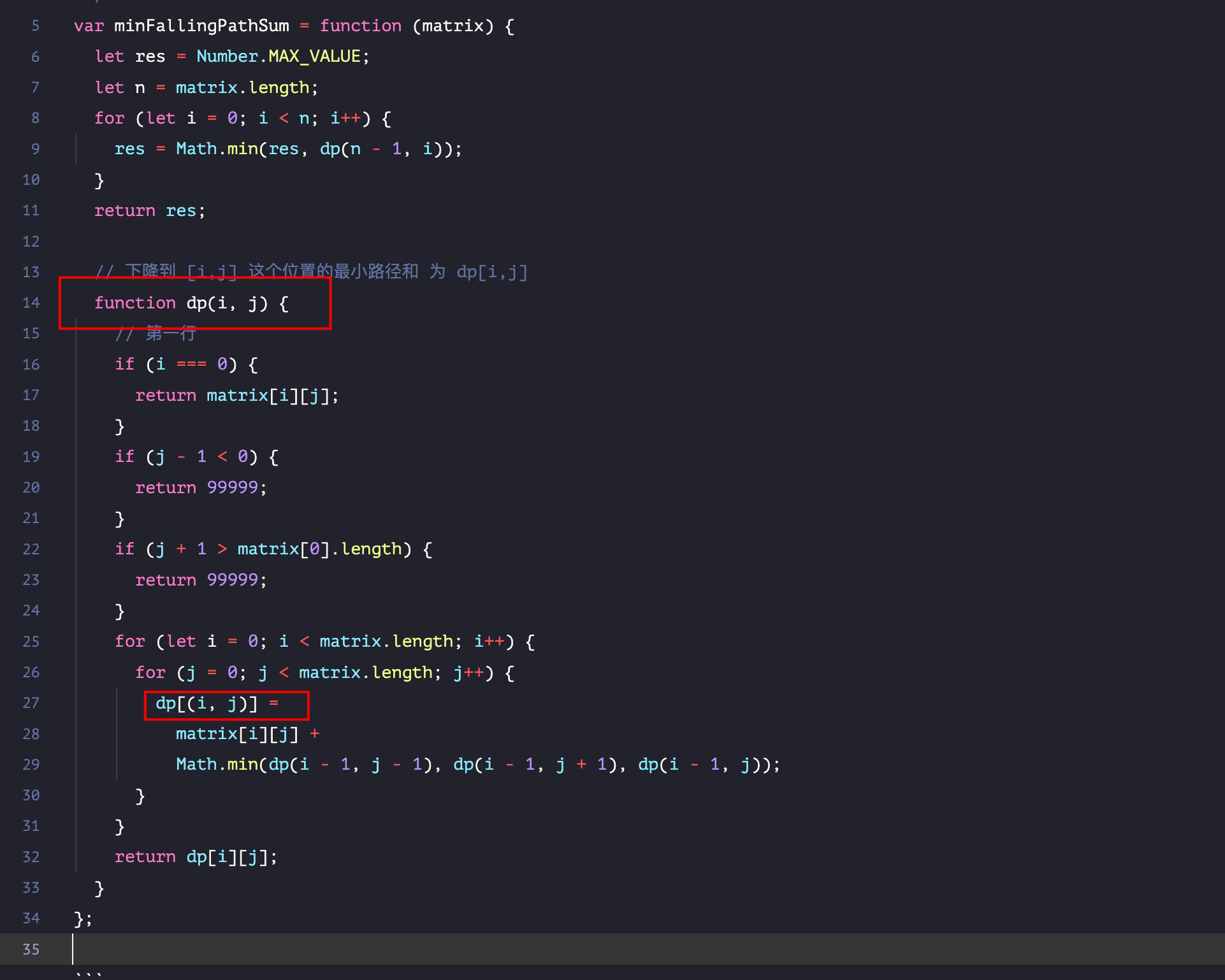
base case 和备忘录的初始值怎么定:下降路径的最小和
#算法/动态规划
目录
1. 总结
1.1. 递归解法
- 定义
dp(i,j):- 下降到
[i,j]这个位置的最小路径和 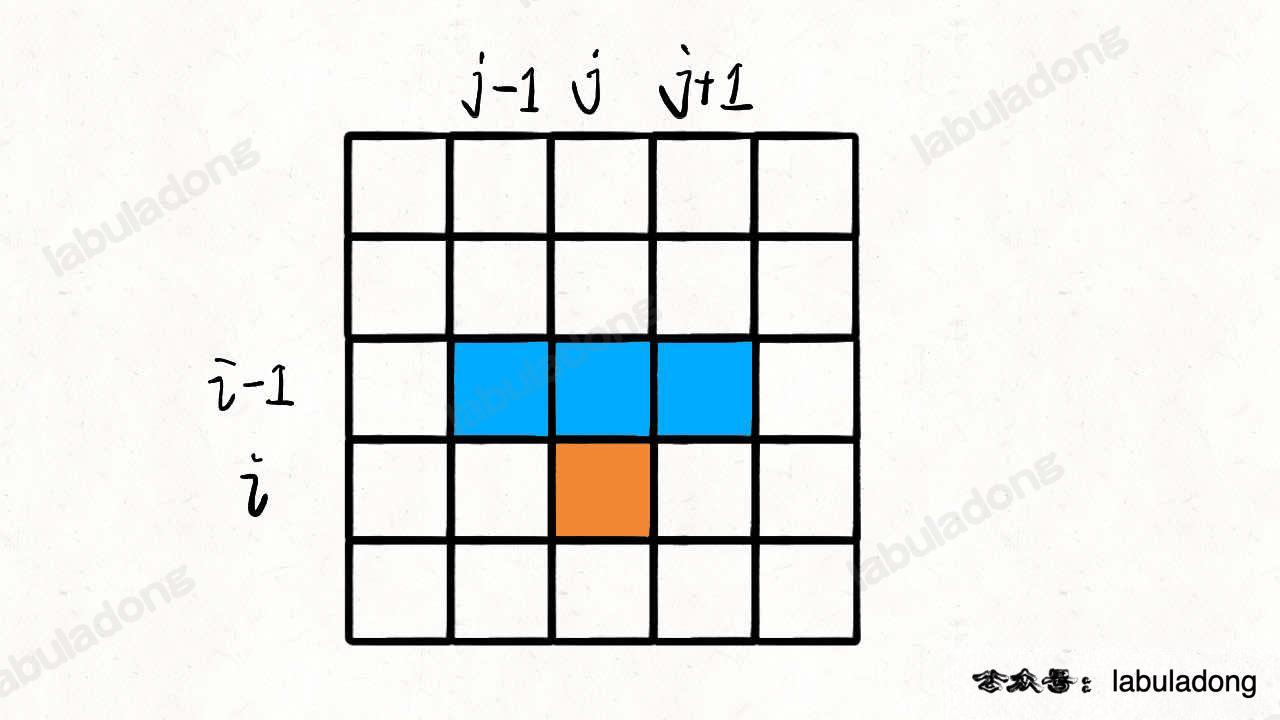
- 下降到
Number.MAX_VALUE这个==好记一点==- 或者看题目设置为
999999y也行
- 或者看题目设置为
- 别和
dp[i][j]搞混了 - 是
n * n - 下面写法不能通过用例,超时了,可以使用备忘录优化
var minFallingPathSum = function (matrix) {
let res = Number.MAX_VALUE;
let n = matrix.length;
for (let i = 0; i < n; i++) {
res = Math.min(res, dp(n - 1, i));
}
return res;
// 下降到 [i,j] 这个位置的最小路径和 为 dp[i,j]
function dp(i, j) {
if (j < 0) {
return 99999;
}
if (j >= n) {
return 99999;
}
// 第一行
if (i === 0) {
return matrix[i][j];
}
return (
matrix[i][j] + Math.min(
dp(i - 1, j - 1),
dp(i - 1, j + 1),
dp(i - 1, j))
);
}
};
1.2. dp 数组解法
- 还是看这张图
var minFallingPathSum = function (matrix) {
let n = matrix.length;
let dp = new Array(n).fill().map(() => {
return new Array(n).fill(99999);
});
for (let j = 0; j < n; j++) {
dp[0][j] = matrix[0][j];
}
console.log("dp:", dp);
for (let i = 1; i < n; i++) {
for (j = 0; j < n; j++) {
if (j === 0) {
dp[i][j] = matrix[i][j] + Math.min(
dp[i - 1][j],
dp[i - 1][j + 1]
);
} else if (j === n - 1) {
dp[i][j] = matrix[i][j] + Math.min(
dp[i - 1][j - 1],
dp[i - 1][j]
);
} else {
dp[i][j] =
matrix[i][j] +
Math.min(
dp[i - 1][j - 1],
dp[i - 1][j],
dp[i - 1][j + 1]
);
}
}
}
let res = Number.MAX_VALUE;
for (let j = 0; j < n; j++) {
res = Math.min(res, dp[n - 1][j]);
}
return res;
};
1.3. 错误记录
- 混合了递归和 dp 数组的写法,搞混了啊
2. 题解
- https://leetcode.cn/problems/minimum-falling-path-sum/
简单说就是,输入为一个 n * n 的二维数组 matrix
- 请你计算从
第一行落到最后一行,经过的路径和最小为多少,如下图:
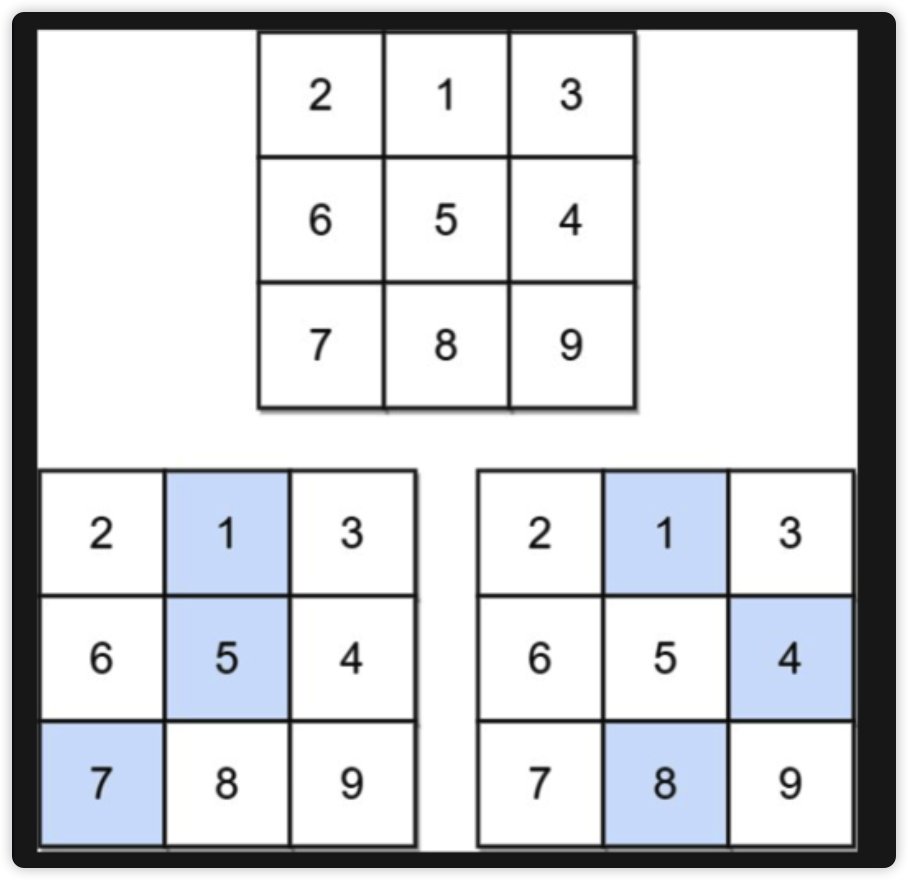
3. dp 函数定义
- 从第一行
matrix[0][?]向下落,落到位置matrix[i][j]的最小路径和为dp(matrix, i, j) - 每次下降,可以
向下、向左下、向右下三个方向移动一格。- 也就是说,可以从
matrix[i][j]降到matrix[i+1][j]或matrix[i+1][j-1]或matrix[i+1][j+1]三个位置。 - 如下图:
橘色的格子只能从三个蓝色的格子转移而来。如下图:
- 也就是说,可以从

所以,只要知道到达 dp(i-1, j), dp(i-1, j-1), dp(i-1, j+1) 这三个位置的最小路径和,加上 matrix[i][j] 的值,就能够计算出来到达位置 (i, j) 的最小路径和:
4. 自顶向下的递归解法 - 暴力
[!info] 1、以下解法,LeetCode 会超时
2、注意下面的所有注释,记录得很详细了
let minFallingPathSum = function (matrix) {
let n = matrix.length;
let res = Number.MAX_VALUE;
// 终点可能在最后一行的任意一列
for (let j = 0; j < n; j++) {
// n-1 即最后一行,j 即最后一行的任意一列
// 所以,只要【遍历】找出落到最后一行的最小路径和,就是最终结果
res = Math.min(res, dp(matrix, n - 1, j));
}
return res;
};
// 从第一行 matrix[0][?] 向下落,
// 落到位置 matrix[i][j] 的最小路径和为 dp(matrix, i, j)
function dp(matrix, i, j) {
// ::::非法索引,返回特殊值
if (i < 0 || i >= matrix.length || j < 0 || j >= matrix.length) {
return 99999;
}
// ::::base case 递归结束条件, 落到第一行的任意一列,返回该列的值
// base: 倒着遍历的,i=0 意味着遍历结束了,触发 base case了
if (i === 0) return matrix[i][j];
// ::::状态转移方程
// ::::从 matrix[i][j] 由三个值转移而来,
// 即 matrix[i-1][j]、matrix[i-1][j-1]、matrix[i-1][j+1] 三个位置
// :::: 注意:都是 i-1,即上一行, j-1、j, j+1 为上一行的左、中、右三个位置
return matrix[i][j] + Math.min(
dp(matrix, i - 1, j),
dp(matrix, i - 1, j - 1),
dp(matrix, i - 1, j + 1)
)
}
const matrix1 = [2, 1, 3], [6, 5, 4], [7, 8, 9](/post/yvkF5tAW.html#2,-1,-3],-[6,-5,-4],-[7,-8,-9);
const matrix2 = [-19, 57], [-40, -5](/post/yvkF5tAW.html#-19,-57],-[-40,--5);
console.log(minFallingPathSum(matrix1)); // 13
console.log(minFallingPathSum(matrix2)); // -59
4.1. 问:为什么要处理非法索引,以及返回特殊值为什么是 99999 ?
首先,递归过程中, i-1 j-1 j+1 这三种运算可能会导致越界,所以需要特殊处理
至于,为什么是 99999 ,看题目,如下图:
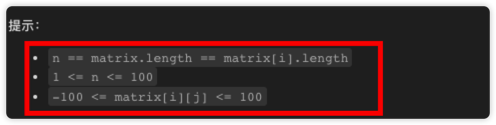
所以,合法答案的区间是 [-10000, 10000],特殊值只要保证是一个永远不会被取到的最大值即可(因为递归的过程中,会重复比较最小值),所以这里使用 > 10001 的任意值都行,当然也包括 99999
4.2. base case 中,为什么是 i===0 ?
dp函数定义所决定的,即 从第一行下落的任意位置下落到位置 matrix[i][j] 的最小路径和为 dp(matrix, i, j)
所以,i === 0
5. 自顶向下的递归解法 - 备忘录优化
代码如下:
/**
* @param {number[][]} matrix
* @return {number}
*/
let minFallingPathSum = function (matrix) {
let n = matrix.length;
let res = Number.MAX_VALUE;
// ::::add 初始化备忘录
let memo = new Array(n).fill([]);
for (let i = 0; i < n; i++) {
memo[i] = new Array(n).fill(66666);
}
// 终点可能在最后一行的任意一列
for (let j = 0; j < n; j++) {
// ::::n-1 即最后一行,j 即最后一行的任意一列
// ::::所以,只要【遍历】找出落到最后一行的最小路径和,就是最终结果
res = Math.min(res, dp(matrix, n - 1, j, memo));
}
return res;
};
// 从第一行 matrix[0][?] 向下落,落到位置 matrix[i][j] 的最小路径和为 dp(matrix, i, j)
function dp(matrix, i, j, memo) {
// ::::1、非法索引,返回特殊值
if (i < 0 || i >= matrix.length || j < 0 || j >= matrix.length) {
return 99999;
}
// 2、base case 递归结束条件, 落到第一行的任意一列,返回该列的值
// i = 0 代表落到第一列,是倒着遍历的,所以是 base case 了
if (i === 0) return memo[i][j] = matrix[i][j];
// ::::3、备忘录
if (memo[i][j] !== 66666) return memo[i][j];
// ::::状态转移方程
// ::::从 matrix[i][j] 由三个值转移而来,
// 即 matrix[i-1][j]、matrix[i-1][j-1]、matrix[i-1][j+1] 三个位置
// :::: 注意:都是 i-1,即上一行, j-1、j, j+1 为上一行的左、中、右三个位置
return memo[i][j] = matrix[i][j] + Math.min(
dp(matrix, i - 1, j, memo),
dp(matrix, i - 1, j - 1, memo),
dp(matrix, i - 1, j + 1, memo)
)
}
const matrix1 = [2, 1, 3], [6, 5, 4], [7, 8, 9](/post/yvkF5tAW.html#2,-1,-3],-[6,-5,-4],-[7,-8,-9);
const matrix2 = [-19, 57], [-40, -5](/post/yvkF5tAW.html#-19,-57],-[-40,--5);
console.log(minFallingPathSum(matrix1)); // 13
console.log(minFallingPathSum(matrix2)); // -59
5.1. 如何初始化一个二维数组,竟然搞不会了?
,假如设置一个 m*n 的二维数组
- 第一、设置
行,初始化元素为空数组new Array(m).fill([]) - 第二,设置
列,根据列m遍历,设置每个元素的值为new Array(n).fill(666)
let m = 3;
let n = 4;
// :::: 首次,new Array(m).fill([])
let memo = new Array(m).fill([]);
// :::: 其次: 根据 n 遍历,并 fill(666)
for (let i = 0; i < m; i++) {
memo[i] = new Array(n).fill(666);
}
console.log(memo);
// 输出如下,3 行 4 列
[
[ 666, 666, 666, 666 ],
[ 666, 666, 666, 666 ],
[ 666, 666, 666, 666 ]
]
[!danger] 注意:每次都使用
行数 m来遍历,最后才会使用列数 n
5.2. 为什么 memo 的初始化值为 66666 ?
同样,这个==问题==的 合法区域是 [-10000, 10000] ,所以,初始化值只要避开这个区间即可,当然,66666 就是在这个区间外
6. 自低向上的 dp数组 解法
见上面总结部分
7. 参考
- https://labuladong.github.io/algo/di-er-zhan-a01c6/dong-tai-g-a223e/basecase-h-de925/
- https://leetcode.cn/problems/minimum-falling-path-sum/