跳跃游戏 II

#leetcode #算法/动态规划 #算法/贪心算法

1. 总结

贪心算法
- 每次跳跃都选择【下一个位置】能跳的最远的地方
动态规划
- dp[i]
  - 从 nums[i] 跳到最后，至少需要 dp[i] 步
    - dp[i] = Math.min(dp[i], dp[j] + 1);

var jump = function (nums) {
  let n = nums.length;
  // 从 nums[i] 跳到最后，至少需要 dp[i] 步
  let dp = new Array(n).fill(Number.MAX_VALUE);

  // 站在最后一个位置，不需要跳
  dp[n - 1] = 0;

  for (let i = n - 2; i >= 0; i--) {
    // 站在当前位置，最多能跳 i + num[i] ，但也不能超过数组长度
    let m = Math.min(i + nums[i], n - 1);
    // 从所有可能的跳跃中选择最小步数
    for (let j = i + 1; j <= m; j++) {
      dp[i] = Math.min(dp[i], dp[j] + 1);
    }
  }
  return dp[0];
};

2. 题目及理解

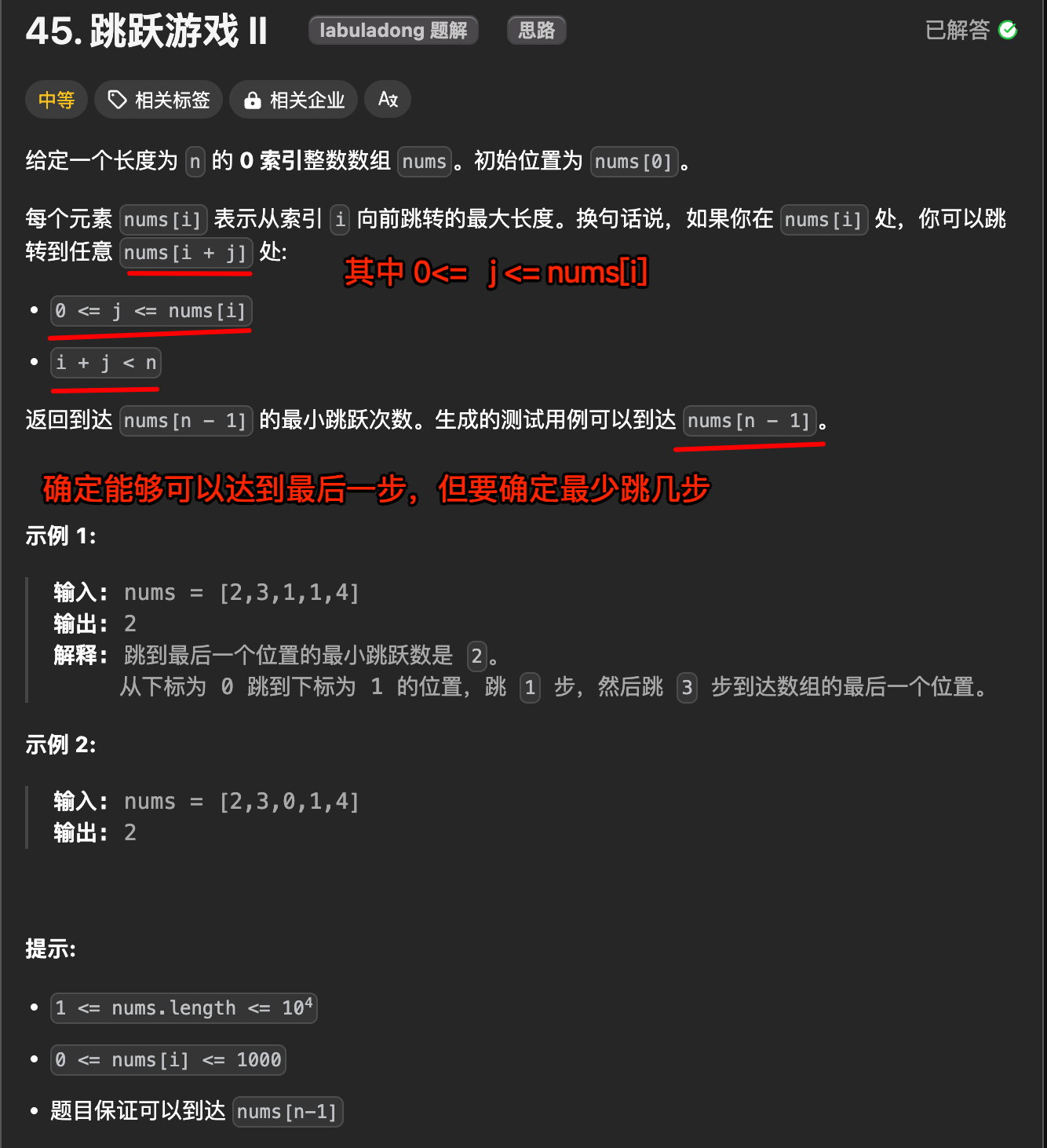
cos-blog-832-34-20241012|680

保证你一定可以跳到最后一格，请问你最少要跳多少次，才能跳过去

3. 思路一：动态规划

3.1. `dp` 函数定义

从索引 p 跳到最后一格，至少需要 dp(nums, p) 步

3.2. 动态规划框架模板

/**  
 * @param {number[]} nums  
 * @return {number}  
 */  
var jump = function (nums) {  
    const len = nums.length;  
    // 默认值是 len, 因为最坏的情况就是每次只跳 1 步,最大步数就是 len - 1
    // len 代表不可达  
    const memo = new Array(len).fill(len);  
    return dp(nums, 0, memo);  
  
};  
  
/**  
 * @description dp(nums, i, memo) 表示从第 i 个位置跳到最后一个位置所需要的最少步数  
 * @param {number[]} nums 跳跃数组  
 * @param {number} i 当前位置  
 * @param {number[]} memo 备忘录  
 * */  
function dp(nums, i, memo) {  
    // ... 待补充  
}

3.3. 代码实现

/**
 * @param {number[]} nums
 * @return {number}
 */
var jump = function (nums) {

    const len = nums.length;
    // 默认值是 len, 因为最坏的情况就是每次只跳 1 步,最大步数就是 len - 1
    // len 代表不可达
    const memo = new Array(len).fill(len);

    return dp(nums, 0, memo);

};

/**
 * @description dp(nums, i, memo) 表示从第 i 个位置跳到最后一个位置所需要的最少步数
 * @param {number[]} nums 跳跃数组
 * @param {number} i 当前位置
 * @param {number[]} memo 备忘录
 * */
function dp(nums, i, memo) {
    // base case
    const len = nums.length;
    if (i >= len - 1) {
        return 0;
    }
    // 之前已经计算过，直接返回备忘录的值
    if (memo[i] !== len) {
        return memo[i];
    }
    // 当前位置最多能跳的步数
    const steps = nums[i];
    // 从当前位置跳 steps 步
    for (let step = 1; step <= steps; step++) {
        // 下一个位置
        const next = i + step;
        // 递归求解
        const subProblem = dp(nums, next, memo);
        // 更新 memo
        memo[i] = Math.min(memo[i], 1 + subProblem);
    }
    // 返回 memo[i]
    return memo[i];
}

3.4. 复杂度分析

时间复杂度：O(n * m)，其中 n 是数组长度，m 是数组中的最大值。但由于使用了记忆化，实际运行时间通常会更优。
空间复杂度：O(n)

上面的复杂度很高的，有没有更高效的算法，见下面的贪心算法题解

4. 思路二：贪心算法

我们不需要像#2.1. 解题思路一：动态规划那样真的「递归地」穷举出所有选择的具体结果来比较求最值，而只需要每次选择那个最有潜力的局部最优解，最终就能得到全局最优解。

4.1. 一个形象的例子

想象你正在玩一个跳石头过河的游戏：
- 河面上有一排石头，每个石头上有一个数字，表示你从这个石头最远可以跳多远。
- 你的目标是用最少的跳跃次数到达最后一个石头。
- 你总是可以到达最后一个石头。
贪心算法的核心思想是：每次跳跃时，都要选择能够使你在下一跳到达最远位置的石头。
例子：
- 假设石头上的数字是 [2, 3, 1, 1, 4]
- 第 0 个石头（值为 2）：
  - 你站在第一个石头上，可以跳 1 步或 2 步。
  - 如果跳 1 步到索引 1，下一跳最远可以到达索引 4（1 + 3 = 4）。
  - 如果跳 2 步到索引 2，下一跳最远只能到达索引 3（2 + 1 = 3）。
  - 贪心选择：跳到索引 1（值为 3 的石头），因为它能让你下一跳到达最远。
- 第 1 个石头（值为 3）：
  - 你现在在索引 1，可以跳 1、2 或 3 步。
  - 但是不管跳几步，都能直接到达最后一个石头。
  - ==贪心选择：直接跳到最后一个石头。==
- 总跳跃次数：2 次

这就像是在玩看得最远跳得最远 的游戏。每次跳跃，你都==选择一个能让你在下一跳看得最远的地方==。这样，你就能用最少的跳跃次数到达终点。

==这个贪心策略之所以有效，是因为题目保证了总是可以到达最后一个位置。所以我们不需要担心会跳到一个“死胡同“，只需要专注于如何跳得最远==。

4.2. 再看例子，如下图

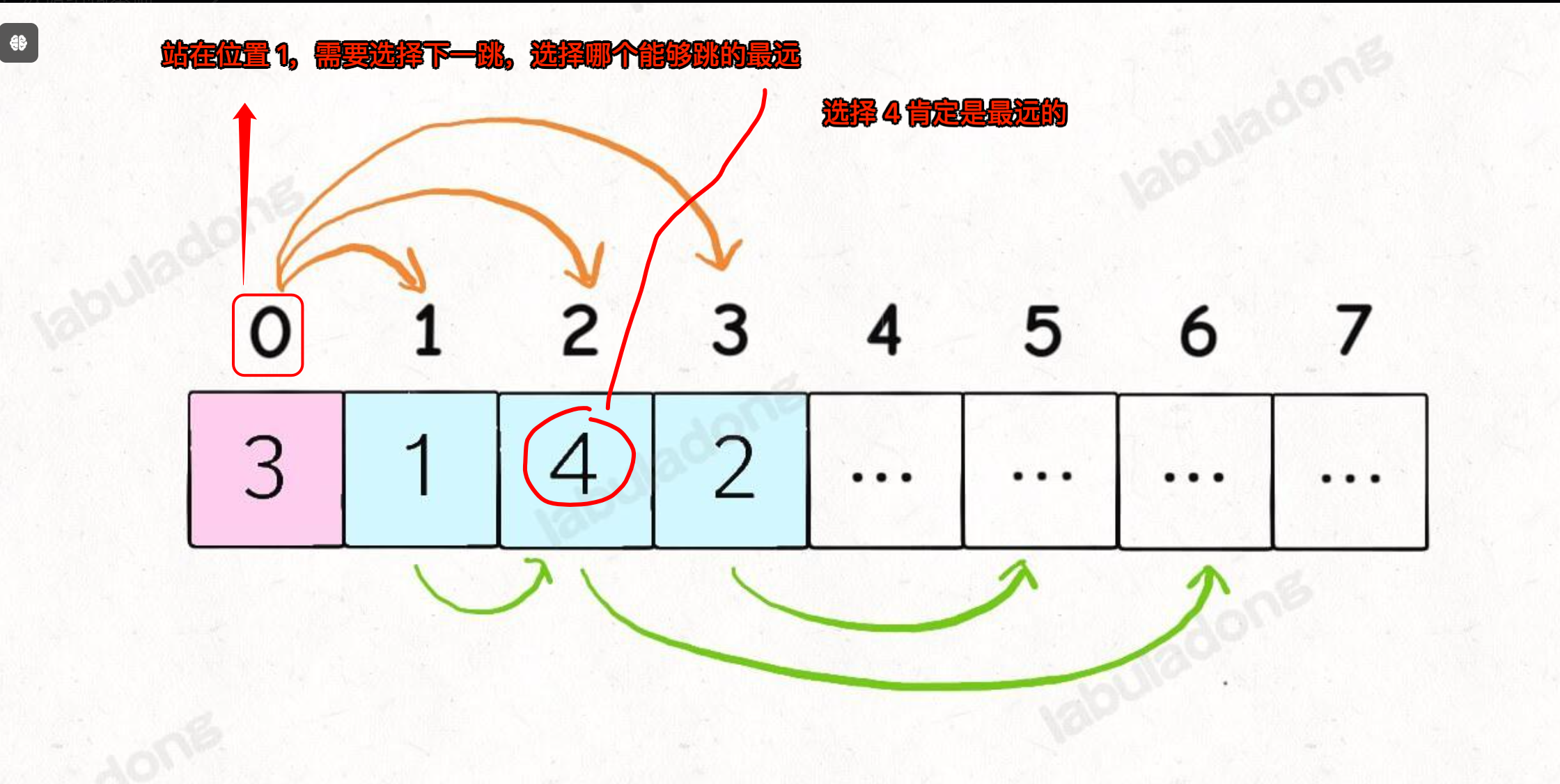
cos-blog-832-34-20241012

5. 代码实现

/**
 * @description 贪心算法解法
 * @param {number[]} nums
 * @return {number}
 */
var jump = function (nums) {
    const len = nums.length;
    // 当前位置，表示当前所在的位置，已经跳到了哪里，即索引
    let currentPosition = 0;
    // 步数，不是数组，而是一个数
    let stepsNum = 0;
    // 能跳的最远距离
    let maxJump = 0;

    // 注意这里是小于 len - 1, 因为最后一个位置不用跳
    // 每次跳跃都选择【下一个位置】能跳的最远的地方
    for (let i = 0; i < len - 1; i++) {
        // 更新 maxJump
        // 下个跳跃位置能够到达的最远距离为 【i + nums[i]】
        maxJump = Math.max(maxJump, i + nums[i]);
        // 到达当前位置的时候，更新 currentPosition
        if (i === currentPosition) {
            currentPosition = maxJump;
            stepsNum++;
        }
    }
    // 返回结果
    return stepsNum;
};

6. 复杂度分析

时间复杂度：O(n)
- 其中 n 是输入数组的长度。
空间复杂度：O(1)
- 算法只使用了几个额外的变量（currentPosition, stepsNum, maxJump），这些都是常数级的额外空间。
- 没有使用任何与输入规模相关的额外数据结构。

liguwe's site