二叉树算法概述

#算法/二叉树

1. 总结
2. 二叉树的重要性
3. 真正理解二叉树的前后中遍历
4. 二叉树的两种解题思路
5. 二叉树的最大深度
- 5.1. 思路 1：遍历一遍二叉树的思路
- 5.2. 思路 2：分解问题的思路
6. 问：如何通过前序遍历打印是所有节点
7. 后序位置与前序位置真正区别？
- 7.1. 如何打印出每一个节点所在的层数 ？
- 7.2. 如何打印出每个节点的左右子树各有多少节点？
9. 层次遍历
- 9.1. 解法 1：前序遍历的思路
- 9.2. 那么，层序遍历（或 BFS 思路）的解法呢？
10. 最后，再总结二叉的解题思路

1. 总结

二叉树的重要性：只要涉及到递归，就是二叉树问题
理解二叉树的前后中序遍历
二叉树的两种解法
示例：二叉树的最大深度
示例：求解二叉树的直径
层次遍历：其实就是 BFS

2. 二叉树的重要性

二叉树模型几乎是所有高级算法的基础，换句话来说，递归有多重要，那么二叉树就有多重要

[!info] 自己想想 递归 有多重要

甚至可以说，只要涉及 递归，都可以抽象成二叉树的问题。

3. 真正理解二叉树的`前后中遍历`

3.1. 教科书中的二叉树遍历

前序遍历（根 => 左 => 右）
- 对于树中的任意节点来说，先访问这个节点本身，然后再访问它的左子树，最后访问它的右子树
- 场景： 输出某个文件夹下所有文件名称(可以有子文件夹)
中序遍历（左 => 根 => 右）
- 对于树中的任意节点来说，先访问它的左子树，然后再访问它的本身，最后访问它的右子树
- 应用： 比如对二叉搜索树进行排序
后序遍历（左 => 右 => 根）
- 对于树中的任意节点来说，先访问它的左子树，然后再访问它的右子树，最后访问它本身
- 应用： 需要根据 左右子树的信息 去执行操作，比如删除节点，又比如统计某个文件夹的大小 ，你就得知道它下面所有文件或者文件夹的大小。

比如前后遍历的代码如下：

image.png|525

3.1.1. 二叉树遍历框架：关注三个位置即可

function traverse(root) {
    if (root == null) {
        return;
    }
    /*************************************************
     * ::::前序位置::::
     ************************************************/
    traverse(root.left);
    /*************************************************
     * ::::中序位置::::
     ************************************************/
    traverse(root.right);
    /*************************************************
     * ::::后序位置::::
     ************************************************/
}

那么，你真正理解了前后中遍历了吗？比如，快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历 ，你如何理解？

3.2. `快速排序`就是二叉树的`前序遍历`

代码框架：

var sort = function (nums, lo, hi) {
    /*************************************************
     * ::::前序位置::::
     ************************************************/
    // 通过交换元素构建分界点 p
    var p = partition(nums, lo, hi);

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
};

3.3. `归并排序` 就是二叉树的`后序遍历`

代码框架：

// 定义：排序 nums[lo..hi]
function sort(nums, lo, hi) {
  if (lo == hi) {
    return;
  }
  
  var mid = Math.floor((lo + hi) / 2);
  // 递归1:  利用定义，排序 nums[lo..mid]
  sort(nums, lo, mid);
  // 递归2:  利用定义，排序 nums[mid+1..hi]
  sort(nums, mid + 1, hi);

  /****** 后序位置 ******/
  // 合并两个有序数组，
  merge(nums, lo, mid, hi);

}
function merge(nums, lo, mid, hi);

3.4. 说回遍历框架：前中序究竟代表什么？

var traverse = function(root) {
    if (root === null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

以上遍历框架，只是一个能够遍历二叉树所有节点的一个函数 traverse 而已，和遍历数组、链表没有任何区别。如下：


// 迭代遍历：for循环 遍历数组
var traverse = function(arr){
    for (var i=0; i<arr.length; i++) {
        // Code block to be executed
    }
}
// 递归遍历： 遍历数组
var traverse = function(arr, i){
    if (i == arr.length) {
        return;
    }
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}
// 迭代遍历：for循环 遍历链表
var traverse = function(head){
    for (var p = head; p != null; p = p.next) {
        // Code block to be executed
    }
}
//  递归遍历： 遍历链表
var traverse = function(head){
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

所以，有以下结论：

遍历有两种方式： 迭代遍历 和 递归遍历
二叉树这种结构无非就是二叉链表，没法通过迭代遍历
递归遍历，有前序 和 后序两个位置
1. 前序位置是刚进入节点时
2. 后序则是即将离开节点时

下图展示了一个单链表的遍历流程，绿色代表进入节点，即前序位置，红色代表 后序 位置。

所以，如果想要 倒序 打印单链表，利用递归遍历单链表，并在后续位置log即可，其本质是利用递归的堆栈能力。如下代码：

/* 递归遍历单链表，倒序打印链表元素 */
var traverse = function(head) {
    if (head === null) {
        return;
    }
    // 前序位置什么也不用做
    traverse(head.next);
    // 后序位置 打印
    console.log(head.val);
}

二叉树相比较于单链表，多了一个 中序位置，如下图：

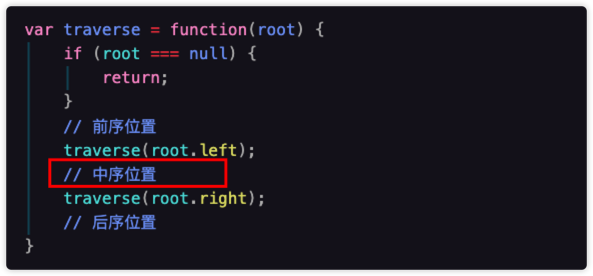
image.png|569

3.4.1. 总结：`前中后序遍历二叉树`的`真正区别`是什么？

1、前序位置的代码 在刚刚进入一个二叉树节点的时候执行； 2、后序位置的代码 在将要离开 一个二叉树节点的时候执行； 3、中序位置的代码 在一个二叉树节点左子树都遍历完，即将开始遍历其右子树的时候执行。如下图：

image.png|540

通过上图可以发现，遍历二叉树的每个节点都有「唯一」属于自己的前中后序位置。而多叉树，没有唯一的中序遍历位置，所以不存在多叉树中序遍历（多叉树节点可能有很多子节点，会多次切换子树去遍历）

最后， 二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作

[!info] 这就是递归的意义，代码框架好了后，递归会帮你做，你的小脑袋瓜子别尝试去理解递归，那是计算机的东西，你搞不过他。

4. 二叉树的`两种解题思路`

遍历一遍二叉树得出答案
通过分解问题计算出答案

这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。看如下解释：

二叉树中用遍历思路解题时函数签名一般是 void traverse(...)，没有返回值，靠更新外部变量来计算结果；
- 而回溯算法核心框架 中给出的函数签名一般也是 没有返回值的 void backtrack(...)
分解问题思路解题时函数名根据该函数具体功能而定
- 而且一般会有返回值，返回值是子问题的计算结果；
- 而 动态规划核心框架中给出的函数签名是带有返回值的 dp 函数

5. 二叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-binary-tree/

5.1. 思路 1：遍历一遍二叉树的思路

即 遍历一遍二叉树

用一个外部变量 res记录每个节点所在的深度
变量depth 记录当前递归到的节点深度

最后，取 depth 和 res 的最大值就可以得到最大深度，代码如下：

var maxDepth = function(root) {
    let res = 0;
    // depth 记录当前递归到的节点深度
    let depth = 0;
    function traverse(root) {
        if(root === null) return;
        depth++;
        // 到达叶子节点
        if(root.left === null && root.right === null){
            res = Math.max(depth, res);
        }
        traverse(root.left);
        traverse(root.right);
        depth--;
    }
    traverse(root);
    return res;
};

[!info] 注意：函数命名和框架 traverse ，这种规范的好处是直接套用就行，主要精力放在具体逻辑上就好，架子的东西都是个人习惯，但要统一，不然给自己添加成本

5.2. 思路 2：分解问题的思路

即通过子树的最大深度推导出原树的深度，所以必然主要逻辑都在 后序位置，因为后序位置能够得到子树的深度。

var maxDepth = function (root) {
    if (root == null) {
        return 0;
    }
    // 利用定义，计算左右子树的最大深度
    var leftMax = maxDepth(root.left);
    var rightMax = maxDepth(root.right);
    // 整棵树的最大深度等于左右子树的最大深度取最大值，
    // 然后再加上根节点自己
    var res = Math.max(leftMax, rightMax) + 1;
    return res;
};

6. 问：如何通过`前序遍历`打印是所有节点

https://leetcode.cn/problems/binary-tree-preorder-traversal/

同样需要借助外部变量 res，如下代码：

var res = [];

// 返回前序遍历结果
function preorderTraverse(root) {
  traverse(root);
  return res;
}

// 二叉树遍历函数
function traverse(root) {
  if (root === null) {
    return;
  }
  // 前序位置
  res.push(root.val);
  traverse(root.left);
  traverse(root.right);
}

中序和后序同理。上面代码的位置变一变即可

7. 后序位置与前序位置真正区别？

位置很重要，比如你如何理解

前序位置的代码执行是自顶向下的，
而后序位置的代码执行是自底向上，看下图：

image.png|416

意味着

前序位置的代码只能从函数参数中获取父节点传递来的数据，
而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据

看两个例子：

7.1. 如何打印出每一个节点所在的`层数` ？

[!tip]

作为参数往下传递即可

一个节点在第几层，你从根节点遍历过来的过程就能 顺带记录，用递归函数的参数就能传递下去，所以放在前序位置和后续位置都行，因为都可以通过递归函数作为参数传递。

/**
 * @param {TreeNode} root
 * @param level 当前节点所在的层数
 * */
function traverse(root, level) {
    if (root == null) {
        return;
    }
    console.log(`节点 ${root} 在第 ${level} 层`);
    // 前序位置
    traverse(root.left, level + 1);
    traverse(root.right, level + 1);
}

traverse(root, 1);

7.2. 如何打印出每个节点的`左右子树`各有多少节点？

而以一个节点为根的整棵子树有多少个节点，你需要遍历完子树之后才能数清楚，然后通过递归函数的返回值拿到答案。所以必然需要放在 后序位置

var count = function(root) {
    if (root === null) {
        return 0;
    }
    var leftCount = count(root.left);
    var rightCount = count(root.right);
    // 后序位置
    console.log("节点 " + root + " 的左子树有 " + leftCount + " 个节点，右子树有 " + rightCount + " 个节点");

    return leftCount + rightCount + 1;
}

[!info] 一旦你发现题目和 子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

9. 层次遍历

image.png|426

如下图： image.png|576

9.1. 解法 1：前序遍历的思路

var levelTraverse = function(root) {
    const res = [];
    traverse(root, 0);
    return res;
    
    // 遍历二叉树的每一层，将每层结点的值存储到 res 中
    function traverse(root, depth) {
        if (!root) {
            return;
        }
        // 当前层数还未被存储过，则初始化对应层的数组
        if (res.length <= depth) {
            res.push([]);
        }
        // 将节点值存储到对应的层数中
        res[depth].push(root.val);
        // 递归遍历左右子节点
        traverse(root.left, depth + 1);
        traverse(root.right, depth + 1);
    }
};

// 其实中序和前序都行
var levelOrder = function(root) {
    const result = [];
    const traverse = (node, layer) => {
        if(node === null){
            return;
        }  
        traverse(node.left, layer + 1);
        /********** 中序位置 start ********** */ 
        if(result[layer]){
            result[layer].push(node.val)
        }else{
            result[layer] = [node.val]
        }
        /************ 中序位置 end ********** */ 
        traverse(node.right, layer + 1);
    }
    traverse(root, 0);
    return result;
};

该解法，本质还是二叉树的前序遍历，或者说 DFS 的思路，而不是层序遍历（或 BFS 思路），因为这个解法是依赖前序遍历自顶向下、自左向右的顺序特点得到了正确的结果。

抽象点说，这个解法更像是从左到右的「列序遍历」，而不是自顶向下的「层序遍历」

9.2. 那么，层序遍历（或 BFS 思路）的解法呢？

BFS 算法框架 就是从二叉树的层序遍历扩展出来的

10. 最后，再总结二叉的解题思路

综上，遇到一道二叉树的题目时的通用思考过程是：

1、是否可以通过 遍历一遍 二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。这叫【「遍历」的思路】。

2、是否可以定义一个 递归函数，通过 子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。【分解问题的思路】

3、无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。递归函数 会帮你在所有节点上执行相同的操作，你的小脑袋瓜子不用去尝试理解递归？

liguwe's site