最大子数组和

#leetcode #2024/08/18 #算法/动态规划 #算法/滑动窗口 #算法/前缀和

目录

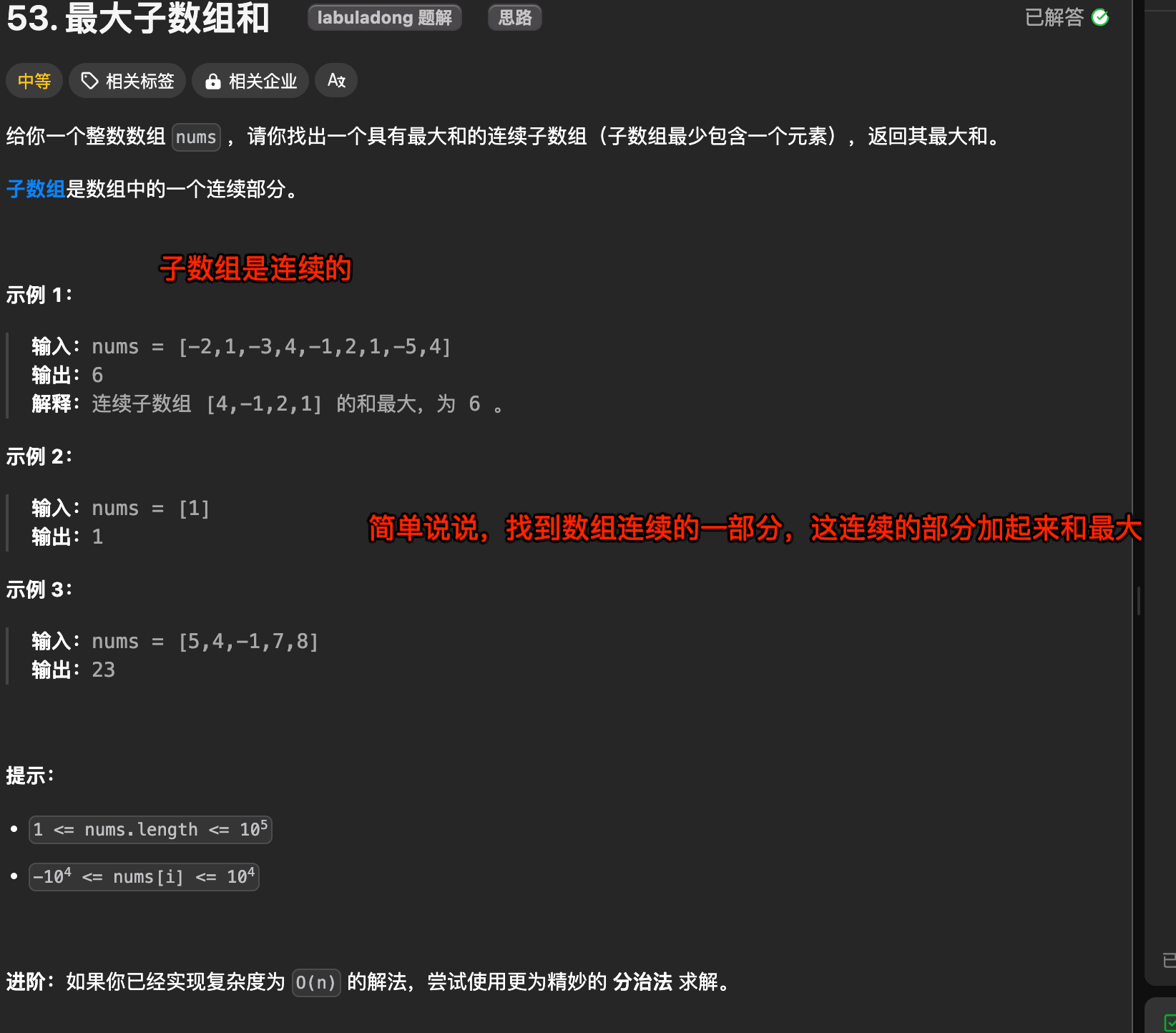
• 1. 题目及理解
• 2. 思路一：前缀和思路
  • 2.1. 思路描述
  • 2.2. 代码实现
  • 2.3. 复杂度分析
  • 2.4. 错误记录
• 3. 思路二：动态规划思路
  • 3.1. dp 定义
  • 3.2. 状态转移方程
  • 3.3. 代码实现
  • 3.4. 复杂度分析
• 4. 思路三：滑动窗口
  • 4.1. 思路
  • 4.2. 代码实现
  • 4.3. 复杂度分析
• 5. 参考

1. 题目及理解

2. 思路一：前缀和思路

2.1. 思路描述

前缀和数组 preSum 就是 nums 元素的累加和

• preSum[i+1] - preSum[j] 其实就是子数组 nums[j..i] 之和（根据 preSum 数组的实现，索引 0 是占位符，所以 i 有一位索引偏移）
• 那么反过来想，以 nums[i] 为结尾的最大子数组之和是多少？
  • 其实就是 preSum[i+1] - min(preSum[0..i])
  • 最大子数组和 = 当前位置的前缀和 - 最小前缀和， 所以设置两个变量
    • res 代表 最大子数组和
    • minPreSum 代表 当前位置之前的最小前缀和

[!danger] 注意是：preSum[i+1] - minPreSum ，不是 preSum[i]

2.2. 代码实现

/**  
 * @description 最大子数组和，前缀和思路  
 * @param {number[]} nums  
 * @return {number} 返回最大子数组和  
 */  
var maxSubArray = function (nums) {  
    /*************************************************  
     * ::::::::::::::::: 构造前缀和 ::::::::::::::::::  
     ************************************************/  
    let preSum = [0];  
    /*************************************************  
     * ::::① 注意 i 从 1 开始，因为前缀和数组的第一个元素是 0::::  
     * ::::② i <= nums.length，因为前缀和数组的长度是 nums.length + 1::::  
     ************************************************/  
    for (let i = 1; i <= nums.length; i++) {  
        preSum[i] = preSum[i - 1] + nums[i - 1];  
    }  
    /*************************************************  
     * ::::当前的最大子数组和，初始化为最小值::::  
     * ::::即 Number.MIN_VALUE 或者 初始化题设中的最小值即可::::  
     ************************************************/  
    let res = -10000 * 100000;  
    /*************************************************  
     * ::::当前位置之前的最小前缀和，初始化最大值 ::::  
     ************************************************/  
    let minPreSum = 10000 * 100000;  
    // 最大子数组和 = 当前位置元素的前缀和 - 最小前缀和  
    for (let i = 0; i < nums.length; i++) {  
        // 更新最小前缀和  
        minPreSum = Math.min(minPreSum, preSum[i]);  
        //公式：最大子数组和 = 当前位置元素的前缀和 - 最小前缀和  
        res = Math.max(res, preSum[i + 1] - minPreSum);  
    }  
    return res;  
};

2.3. 复杂度分析

• 时间复杂度是 O(n)，其中 n 是数组的长度，因为我们只遍历了数组一次
• 空间复杂度是 O(1)，因为我们只使用了常数额外空间

2.4. 错误记录

• 如何初始化一个 preSum ? 得没有意识的就得写对

3. 思路二：动态规划思路

3.1. dp 定义

• 以 nums[i] 为结尾的「最大子数组和」为 dp[i]。
• dp[i] 有两种「选择」，
  • 要么与前面的相邻子数组连接，形成一个和更大的子数组
  • 要么不与前面的子数组连接，自成一派，自己作为一个子数组

3.2. 状态转移方程

依然使用数学归纳法来找状态转移关系：假设我们已经算出了 dp[i-1]，如何推导出 dp[i] 呢？

// 要么自成一派，要么和前面的子数组合并 
var dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);

3.3. 代码实现

• ① dp[i] 表示以 nums[i] 结尾的连续子数组的最大和
• ② base case
• ③ 遍历，使用状态转移方程得到 dp 数组
• ④ 遍历 dp 数组，找到最大值

/**  
 * @description 最大子数组和，动态规划思路  
 * @param {number[]} nums  
 * @return {number} 返回最大子数组和  
 */  
var maxSubArray = function (nums) {  
    // ①  dp[i] 表示以 nums[i] 结尾的连续子数组的最大和  
    let dp = new Array(nums.length);  
    // ②  base case    dp[0] = nums[0];  
    // ③ 遍历，使用状态转移方程得到 dp 数组  
    for (let i = 1; i < nums.length; i++) {  
        dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);  
    }  
    // ④  遍历 dp 数组，找到最大值 
    let res = -10000 * 100000;   
    for (let i = 0; i < dp.length; i++) {  
        res = Math.max(res, dp[i]);  
    }  
    return res;  
};

3.4. 复杂度分析

时间复杂度分析：

1. 第一个循环：遍历数组填充 dp 数组，需要 O(n) 时间。
2. 第二个循环：遍历 dp 数组找最大值，也需要 O(n) 时间。
3. 总的时间复杂度：O(n) + O(n) = O(n)，其中 n 是输入数组的长度。

空间复杂度分析：

• 使用了一个额外的 dp 数组，长度与输入数组相同。
• 空间复杂度：O(n)

4. 思路三：滑动窗口

4.1. 思路

• 窗口内元素之和大于等于 0 时扩大窗口
• 在窗口内元素之和小于 0 时缩小窗口
• 在每次移动窗口时更新答案

4.2. 代码实现

/**
 * @description 最大子数组和，滑动窗口思路
 * @param {number[]} nums
 * @return {number} 返回最大子数组和
 */
var maxSubArray = function (nums) {
  let res = -10000 * 100000;
  // ①  初始化左指针，右指针，窗口内元素的和
  let left = 0; // 左指针
  let right = 0; // 右指针
  let windowSum = 0; // 窗口内元素的和

  // ②  遍历，使用滑动窗口思路
  while (right < nums.length) {
    // ③  更新 windowSum
    windowSum += nums[right];
    // ④  更新右指针
    right++;
    // ⑤  更新结果
    res = Math.max(res, windowSum);
    // ⑥  判断是否需要收缩左指针
    while (windowSum < 0) {
      // ⑦  更新 windowSum
      windowSum -= nums[left];
      left++;
    }
  }
  return res;
};

4.3. 复杂度分析

时间复杂度分析：

1. 外层 while 循环：右指针 right 从 0 移动到 nums.length，这需要 O(n) 时间。
2. 内层 while 循环：左指针 left 最多也只会从 0 移动到 nums.length。
3. 虽然有嵌套的循环，但每个元素最多被访问两次（一次被加入窗口，一次被移出窗口）。
4. 总的时间复杂度：O(n)，其中 n 是输入数组的长度。 空间复杂度分析：

• 使用了常数额外空间（left, right, windowSum, res）。
• 空间复杂度：O(1)

5. 参考

• https://labuladong.online/algo/dynamic-programming/maximum-subarray